
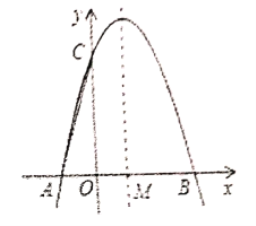
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,抛物线的对称轴
点,抛物线的对称轴![]() 与
与![]() 轴交于
轴交于![]() 点.
点.
(1)求抛物线的函数解析式;
(2)设点![]() 是直线
是直线![]() 上的一个动点,当
上的一个动点,当![]() 的值最小时,求
的值最小时,求![]() 的长;
的长;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,点
(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ,理由见解析
,理由见解析
【解析】
(1)由题意先求得C(0,3).设抛物线的解析式为y=a(x+1)(x-3),将点C的坐标代入可求得a的值即可;
(2)由题意依据轴对称图形的性质可知PA=PB,则PA+PC=PB+PC,则当点P在线段BC上时,PC+AP有最小值,PA+PC的最小值=BC,接下来,依据勾股定理求解即可;
(3)根据题意设点Q的坐标为(1,m),则QM=|m|,然后依据相似三角形的性质可得到∠OQM=∠CAO或∠OQM=∠ACO,然后依据相似三角形的性质列比例求解即可.
解:(1)把![]() 代入抛物线
代入抛物线![]() 中,得
中,得![]()
![]()
设抛物线的解析式为![]()
将点![]() 的坐标代入,得
的坐标代入,得![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
(2)如图所示:
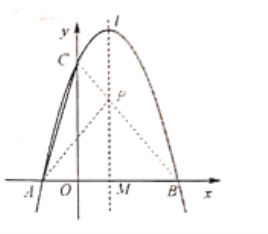
![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,点
对称,点![]() 在直线
在直线![]() 上
上
![]()
![]()
![]() 两点之间线段最短
两点之间线段最短
![]() 当点
当点![]() 在线段
在线段![]() 上时,
上时,![]() 有最小值,
有最小值,
![]() 的最小值即为
的最小值即为![]()
![]() ,
,![]()
![]()
![]() 的最小值为
的最小值为![]() .
.
(3)抛物线的对称轴为直线![]()
设点![]() 的坐标为
的坐标为![]() ,则
,则![]()
![]() 以
以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
![]() 或
或![]()
当![]() 时,
时,![]()
即![]() ,解得
,解得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]()
当![]() 时,
时,![]()
即![]() ,解得
,解得![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]()
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
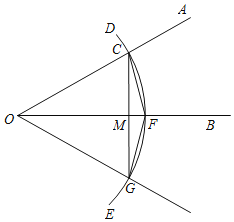
【题目】已知锐角∠AOB如图,
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧DE,交射线OB于点F,连接CF;
(2)以点F为圆心,CF长为半径作弧,交弧DE于点G;
(3)连接FG,CG.作射线OG.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠BOG=∠AOBB.若CG=OC,则∠AOB=30°
C.OF垂直平分CGD.CG=2FG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)直接写出点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)若![]() 两点中只有一个点在线段
两点中只有一个点在线段![]() 上,直接写出
上,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
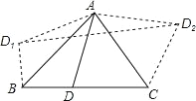
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班![]() 名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
金额/元 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 18 | 10 | 8 | 2 |
A.平均数为![]() 元B.众数为
元B.众数为![]() 元C.中位数为
元C.中位数为![]() 元D.极差为
元D.极差为![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第24届冬奥会将于2022年在北京和张家口举行,冬奥会的项目有滑雪(如高山滑雪、单板滑雪等),滑冰(如速度滑冰、花样滑冰等),冰球,冰壶等.如图,有4张形状、大小、质地均相同的卡片,正面分别印有单板滑雪、速度滑冰、冰球、冰壶4种不同的图案,背面完全相同.现将这4张卡片洗匀后正面向下放在桌子上.

(1)从中随机抽取1张,抽出的卡片上恰好是滑雪项目图案的概率是 .
(2)若印有单板滑雪、速度滑冰、冰球、冰壶4种不同图案的卡片分别用A,B,C,D表示,从中随机抽取两张,试用画树状图或列表的方法求出印有冰球图案的卡片被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com