
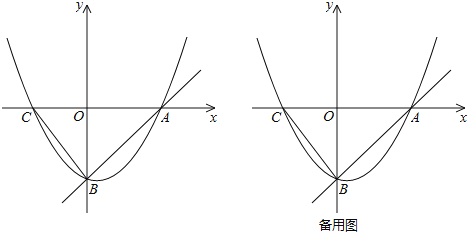
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНxЉ4гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌХзЮяЯпyЃН![]() x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌСЌНгBCЃЎ
x2+bx+cОЙ§AЁЂBСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕуMдкХзЮяЯпЩЯЃЌСЌНгMBЃЌЕБЁЯMBA+ЁЯCBOЃН45ЁуЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉЕуPДгЕуCГіЗЂЃЌбиЯпЖЮCAгЩCЯђAдЫЖЏЃЌЭЌЪБЕуQДгЕуBГіЗЂЃЌбиЯпЖЮBCгЩBЯђCдЫЖЏЃЌPЁЂQЕФдЫЖЏЫйЖШЖМЪЧУПУы1ИіЕЅЮЛГЄЖШЃЌЕБQЕуЕНДяCЕуЪБЃЌPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЌЪдЮЪдкзјБъЦНУцФкЪЧЗёДцдкЕуDЃЌЪЙPЁЂQдЫЖЏЙ§ГЬжаЕФФГвЛЪБПЬЃЌвдCЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкЃЌжБНгаДГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2Љ
x2Љ![]() xЉ4ЃЌCЃЈЉ3ЃЌ0ЃЉЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ
xЉ4ЃЌCЃЈЉ3ЃЌ0ЃЉЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ5ЃЌ
ЃЉЛђЃЈ5ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕуDЃЌЕуDзјБъЮЊЃЈЉ
ЃЉЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕуDЃЌЕуDзјБъЮЊЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈЉ
ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЕквЛЮЪЧѓНтЮіЪНжївЊРћгУД§ЖЈЯЕЪ§ЧѓНтЃЌРћгУвЛДЮКЏЪ§yЃНxЉ4ЃЌЧѓНтГіAЕузјБъКЭBЕузјБъЃЌШЛКѓДњШыЗНГЬМДПЩЃЌ
ЕкЖўЮЪЧѓНтMЕуЕФзјБъЃЌашвЊЬжТлЃЌвђЮЊЁЯMBA+ЁЯCBOЃН45ЁуЪЧЖЏЬЌЕФЃЌЙЪЕБBMЁЭBCЪБЪЧвЛжжЧщПіЃЌРћгУtanЁЯM1BEЃНtanЁЯBCOЃН![]() ЃЌПЩвдИјГіЕШЪНЙиЯЕЃЌЧѓГіMЕуЃЌBMгыBCЙигкyжсЖдГЦЪБЪЧЕкЖўжжЧщПіЃЌtanЁЯM2BEЃНtanЁЯCBOЃН
ЃЌПЩвдИјГіЕШЪНЙиЯЕЃЌЧѓГіMЕуЃЌBMгыBCЙигкyжсЖдГЦЪБЪЧЕкЖўжжЧщПіЃЌtanЁЯM2BEЃНtanЁЯCBOЃН![]() ЃЌПЩвдГіИјЕШЪНЙиЯЕЃЌЧѓГіMЕу
ЃЌПЩвдГіИјЕШЪНЙиЯЕЃЌЧѓГіMЕу
ЕкШ§ЮЪЃЌашвЊЬжТлЃЌвђЮЊЫФИіЕуЃЌжЊЯўЦфжаШ§ИіЕуЃЌПЩвдетбљЬжТлЃЌЕБCPЮЊСтаЮЕФБпЃЌCQЮЊЖдНЧЯпетЪЧЕквЛжжЧщПіЃЌРћгУНтжБНЧШ§НЧаЮЧѓГіQЕуЕФзнзјБъЃЌОЭжЊЕРDЕуЕФзнзјБъЃЌШЛКѓРћгУcosЁЯBCOЃН![]() ЃЌНЈСЂЕШЪНМДПЩЧѓГіСтаЮЕФБпГЄЃЌРћгУСтаЮБпГЄКЭQЕуКсзјБъЃЌМДПЩЕУЕНQЕуКсзјБъЃЌЕБCQКЭCPОљЮЊСтаЮЕФБпетЪЧЕкЖўжжЧщПіЃЌвђЮЊCP=CQ=BQЃЌЫљвдQЕудкBCЕФжаЃЌМДСтаЮЕФБпГЄГіРДСЫЃЌРћгУНтжБНЧШ§НЧаЮМДПЩИјГіQЕуЕФзнзјБъЃЌжЊЕРСтаЮЕФБпГЄЃЌЫљвдDЕуЕФКсзнзјБъЖМГіРДСЫЃЌЕБCQЮЊСтаЮЕФБпЃЌCPЮЊСтаЮЕФЖдНЧЯпетЪЧЕкШ§жжЧщПіЃЌРћгУНтжБНЧШ§НЧаЮЃЌПЩвдИјГіQЕузјБъЃЌЮвУЧПЩвджЊЕРDЕуКЭQЕуЙигкxжсЖдГЦЃЌгаСтаЮЕФЛљБОаджЪПЩвджЊЕРЃЌЫљвдDЕузјБъГіРДСЫ
ЃЌНЈСЂЕШЪНМДПЩЧѓГіСтаЮЕФБпГЄЃЌРћгУСтаЮБпГЄКЭQЕуКсзјБъЃЌМДПЩЕУЕНQЕуКсзјБъЃЌЕБCQКЭCPОљЮЊСтаЮЕФБпетЪЧЕкЖўжжЧщПіЃЌвђЮЊCP=CQ=BQЃЌЫљвдQЕудкBCЕФжаЃЌМДСтаЮЕФБпГЄГіРДСЫЃЌРћгУНтжБНЧШ§НЧаЮМДПЩИјГіQЕуЕФзнзјБъЃЌжЊЕРСтаЮЕФБпГЄЃЌЫљвдDЕуЕФКсзнзјБъЖМГіРДСЫЃЌЕБCQЮЊСтаЮЕФБпЃЌCPЮЊСтаЮЕФЖдНЧЯпетЪЧЕкШ§жжЧщПіЃЌРћгУНтжБНЧШ§НЧаЮЃЌПЩвдИјГіQЕузјБъЃЌЮвУЧПЩвджЊЕРDЕуКЭQЕуЙигкxжсЖдГЦЃЌгаСтаЮЕФЛљБОаджЪПЩвджЊЕРЃЌЫљвдDЕузјБъГіРДСЫ
ЃЈ1ЃЉжБЯпНтЮіЪНyЃНxЉ4ЃЌ
СюxЃН0ЃЌЕУyЃНЉ4ЃЛ
СюyЃН0ЃЌЕУxЃН4ЃЎ
ЁрAЃЈ4ЃЌ0ЃЉЁЂBЃЈ0ЃЌЉ4ЃЉЃЎ
ЁпЕуAЁЂBдкХзЮяЯпyЃН![]() x2+bx+cЩЯЃЌ
x2+bx+cЩЯЃЌ
Ёр
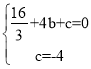 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊЃКyЃН![]() x2Љ
x2Љ![]() xЉ4ЃЎ
xЉ4ЃЎ
СюyЃН![]() x2Љ
x2Љ![]() xЉ4ЃН0ЃЌ
xЉ4ЃН0ЃЌ
НтЕУЃКxЃНЉ3ЛђxЃН4ЃЌ
ЁрCЃЈЉ3ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЁЯMBA+ЁЯCBOЃН45ЁуЃЌ
ЩшMЃЈxЃЌyЃЉЃЌ
ЂйЕБBMЁЭBCЪБЃЌШчД№ЭМ2Љ1ЫљЪОЃЎ
ЁпЁЯABOЃН45ЁуЃЌ
ЁрЁЯMBA+ЁЯCBOЃН45ЁуЃЌЙЪЕуMТњзуЬѕМўЃЎ
Й§ЕуM1зїM1EЁЭyжсгкЕуEЃЌдђM1EЃНxЃЌOEЃНЉyЃЌ
ЁрBEЃН4+yЃЎ
ЁпtanЁЯM1BEЃНtanЁЯBCOЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпBM1ЕФНтЮіЪНЮЊЃКyЃН![]() xЉ4ЃЎ
xЉ4ЃЎ
СЊСЂyЃН![]() xЉ4гыyЃН
xЉ4гыyЃН![]() x2Љ
x2Љ![]() xЉ4ЃЌ
xЉ4ЃЌ
ЕУЃК![]() xЉ4ЃН
xЉ4ЃН![]() x2Љ
x2Љ![]() xЉ4ЃЌ
xЉ4ЃЌ
НтЕУЃКx1ЃН0ЃЌx2ЃН![]() ЃЌ
ЃЌ
Ёрy1ЃНЉ4ЃЌy2ЃНЉ![]() ЃЌ
ЃЌ
ЁрM1ЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
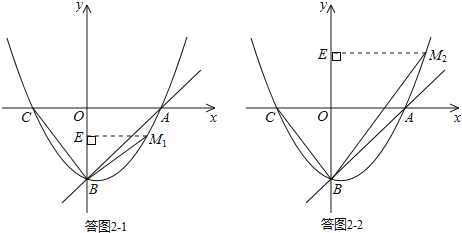
ЂкЕБBMгыBCЙигкyжсЖдГЦЪБЃЌШчД№ЭМ2Љ2ЫљЪОЃЎ
ЁпЁЯABOЃНЁЯMBA+ЁЯMBOЃН45ЁуЃЌЁЯMBOЃНЁЯCBOЃЌ
ЁрЁЯMBA+ЁЯCBOЃН45ЁуЃЌ
ЙЪЕуMТњзуЬѕМўЃЎ
Й§ЕуM2зїM2EЁЭyжсгкЕуEЃЌ
дђM2EЃНxЃЌOEЃНyЃЌ
ЁрBEЃН4+yЃЎ
ЁпtanЁЯM2BEЃНtanЁЯCBOЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпBM2ЕФНтЮіЪНЮЊЃКyЃН![]() xЉ4ЃЎ
xЉ4ЃЎ
СЊСЂyЃН![]() xЉ4гыyЃН
xЉ4гыyЃН![]() x2Љ
x2Љ![]() xЉ4ЕУЃК
xЉ4ЕУЃК![]() xЉ4ЃН
xЉ4ЃН![]() x2Љ
x2Љ![]() xЉ4ЃЌ
xЉ4ЃЌ
НтЕУЃКx1ЃН0ЃЌx2ЃН5ЃЌ
Ёрy1ЃНЉ4ЃЌy2ЃН![]() ЃЌ
ЃЌ
ЁрM2ЃЈ5ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃКЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ5ЃЌ
ЃЉЛђЃЈ5ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉЩшЁЯBCOЃНІШЃЌдђtanІШЃН![]() ЃЌsinІШЃН
ЃЌsinІШЃН![]() ЃЌcosІШЃН
ЃЌcosІШЃН![]() ЃЎ
ЃЎ
МйЩшДцдкТњзуЬѕМўЕФЕуDЃЌЩшСтаЮЕФЖдНЧЯпНЛгкЕуEЃЌЩшдЫЖЏЪБМфЮЊtЃЎ
ЂйШєвдCQЮЊСтаЮЖдНЧЯпЃЌШчД№ЭМ3Љ1ЃЎДЫЪБBQЃНtЃЌСтаЮБпГЄЃНtЃЎ
ЁрCEЃН![]() CQЃН
CQЃН![]() ЃЈ5ЉtЃЉЃЎ
ЃЈ5ЉtЃЉЃЎ
дкRtЁїPCEжаЃЌcosІШЃН![]() ЃН
ЃН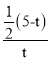 ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрCQЃН5ЉtЃН![]() ЃЎ
ЃЎ
Й§ЕуQзїQFЁЭxжсгкЕуFЃЌ
дђQFЃНCQsinІШЃН![]() ЃЌCFЃНCQcosІШЃН
ЃЌCFЃНCQcosІШЃН![]() ЃЌ
ЃЌ
ЁрOFЃН3ЉCFЃН![]() ЃЎ
ЃЎ
ЁрQЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпЕуD1гыЕуQКсзјБъЯрВюtИіЕЅЮЛЃЌ
ЁрD1ЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
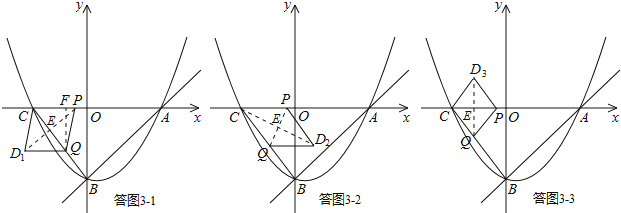
ЂкШєвдPQЮЊСтаЮЖдНЧЯпЃЌШчД№ЭМ3Љ2ЃЎДЫЪБBQЃНtЃЌСтаЮБпГЄЃНtЃЎ
ЁпBQЃНCQЃНtЃЌ
ЁрtЃН![]() ЃЌЕуQЮЊBCжаЕуЃЌ
ЃЌЕуQЮЊBCжаЕуЃЌ
ЁрQЃЈЉ![]() ЃЌЉ2ЃЉЃЎ
ЃЌЉ2ЃЉЃЎ
ЁпЕуD2гыЕуQКсзјБъЯрВюtИіЕЅЮЛЃЌ
ЁрD2ЃЈ1ЃЌЉ2ЃЉЃЛ
ЂлШєвдCPЮЊСтаЮЖдНЧЯпЃЌШчД№ЭМ3Љ3ЃЎДЫЪБBQЃНtЃЌСтаЮБпГЄЃН5ЉtЃЎ
дкRtЁїCEQжаЃЌcosІШЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрOEЃН3ЉCEЃН3Љ![]() tЃН
tЃН![]() ЃЌD3EЃНQEЃНCQsinІШЃНЃЈ5Љ
ЃЌD3EЃНQEЃНCQsinІШЃНЃЈ5Љ![]() ЃЉЁС
ЃЉЁС![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрD3ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌДцдкТњзуЬѕМўЕФЕуDЃЌЕуDзјБъЮЊЃКЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈЉ
ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ


 ЕМбЇгыВтЪдЯЕСаД№АИ
ЕМбЇгыВтЪдЯЕСаД№АИ аТЗЧЗВНЬИЈГхДЬ100ЗжЯЕСаД№АИ
аТЗЧЗВНЬИЈГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
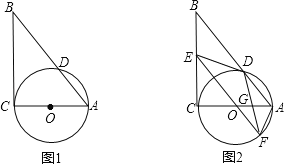
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЎ
(1)дкЭМ(1)жаЃЌгУжБГпКЭдВЙцЙ§ЕуDзїЁбOЕФЧаЯпDEНЛBCгкЕуEЃЛ(БЃСєзїЭМКлМЃЃЌВЛаДзїЗЈ)
(2)ШчЭМ(2)ЃЌШчЙћЁбOЕФАыОЖЮЊ3ЃЌEDЃН4ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЃЌгыOAНЛгкЕуGЃЌЧѓOGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌгавдЯТНсТлЃКЂй
ЕФЭМЯѓШчЭМЫљЪОЃЌгавдЯТНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЦфжаЫљгае§ШЗНсТлЕФађКХЪЧЃЈ ЃЉ
ЦфжаЫљгае§ШЗНсТлЕФађКХЪЧЃЈ ЃЉ

A. ЂйЂк B. ЂйЂлЂм C. ЂйЂкЂлЂн D. ЂйЂкЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
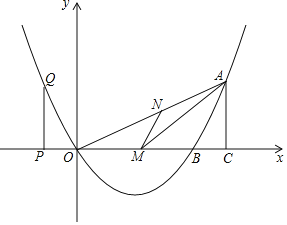
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЙ§ЕуOЃЈ0ЃЌ0ЃЉЃЎAЃЈ8ЃЌ4ЃЉЃЌгыxжсНЛгкСэвЛЕуBЃЌЧвЖдГЦжсЪЧжБЯпxЃН3ЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєMЪЧOBЩЯЕФвЛЕуЃЌзїMNЁЮABНЛOAгкNЃЌЕБЁїANMУцЛ§зюДѓЪБЃЌЧѓMЕФзјБъЃЛ
ЃЈ3ЃЉPЪЧxжсЩЯЕФЕуЃЌЙ§PзїPQЁЭxжсгыХзЮяЯпНЛгкQЃЎЙ§AзїACЁЭxжсгкCЃЌЕБвдOЃЌPЃЌQЮЊЖЅЕуЕФШ§НЧаЮгывдOЃЌAЃЌCЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЪБЃЌЧѓPЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫСЫНтБОаЃ1200УћбЇЩњЕФПЮЭтдФЖСЕФЧщПіЃЌЯжДгИїФъМЖЫцЛњГщШЁСЫВПЗжбЇЩњЖдЫћУЧвЛжмЕФПЮЭтдФЖСЪБМфНјааСЫЕїВщЃЌВЂЛцжЦГіШчЯТЕФЭГМЦЭМЂйКЭЭМЂкЃЌИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
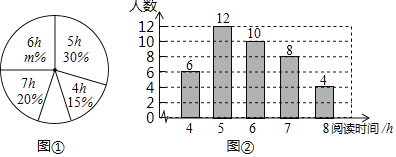
ЃЈ1ЃЉБОДЮНгЪмЫцЛњГщбљЕїВщЕФбЇЩњШЫЪ§ЮЊЁЁ ЭМЂйжаmЕФжЕЮЊЁЁ ЃЛ
ЃЈ2ЃЉБОДЮЕїВщЛёШЁЕФбљБОЪ§ОнЕФжкЪ§ЮЊЁЁ ЃЌжаЮЛЪ§ЮЊЁЁ ЃЛ
ЃЈ3ЃЉЧѓБОДЮЕїВщЛёШЁЕФбљБОЪ§ОнЦНОљЪ§ЃЛ
ЃЈ4ЃЉИљОнбљБОЪ§ОнЃЌЙРМЦИУаЃвЛжмЕФПЮЭтдФЖСЪБМфДѓгк6hЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж10ЗжЃЉШчЭМЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЌACЕФДЙжБЦНЗжЯпЗжБ№гыACЃЌBCМАABЕФбгГЄЯпЯрНЛгкЕуDЃЌEЃЌFЃЌЧвBF=BCЃЎЁбOЪЧЁїBEFЕФЭтНгдВЃЌЁЯEBFЕФЦНЗжЯпНЛEFгкЕуGЃЌНЛгкЕуHЃЌСЌНгBDЁЂFHЃЎ
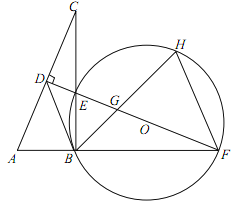
ЃЈ1ЃЉЧѓжЄЃКЁїABCЁеЁїEBFЃЛ
ЃЈ2ЃЉЪдХаЖЯBDгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєAB=1ЃЌЧѓHGHBЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
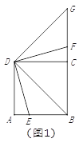
ЁОЬтФПЁПЂХШчЭМ1ЃЌ![]() ЪЧе§ЗНаЮ
ЪЧе§ЗНаЮ![]() Бп
Бп![]() ЩЯЕФвЛЕуЃЌСЌНг
ЩЯЕФвЛЕуЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыа§зЊ90ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯп
ФцЪБеыа§зЊ90ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯп![]() НЛгкЕу
НЛгкЕу![]() КЭЕу
КЭЕу![]() .
.
ЂйЯпЖЮ![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕЪЧ ЃЛ
ЕФЪ§СПЙиЯЕЪЧ ЃЛ
ЂкаДГіЯпЖЮ![]() КЭ
КЭ![]() жЎМфЕФЪ§СПЙиЯЕ.
жЎМфЕФЪ§СПЙиЯЕ.
ЂЦЕБЫФБпаЮ![]() ЮЊСтаЮЃЌ
ЮЊСтаЮЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧСтаЮ
ЪЧСтаЮ![]() Бп
Бп![]() ЫљдкжБЯпЩЯЕФвЛЕуЃЌСЌНг
ЫљдкжБЯпЩЯЕФвЛЕуЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыа§зЊ120ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯп
ФцЪБеыа§зЊ120ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯп![]() НЛгкЕу
НЛгкЕу![]() КЭЕу
КЭЕу![]() .
.
ЂйШчЭМ2ЃЌЕу![]() дкЯпЖЮЩЯЪБЃЌЧыЬНОПЯпЖЮ
дкЯпЖЮЩЯЪБЃЌЧыЬНОПЯпЖЮ![]() КЭ
КЭ![]() жЎМфЕФЪ§СПЙиЯЕЃЌаДГіНсТлВЂИјГіжЄУїЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌаДГіНсТлВЂИјГіжЄУїЃЛ
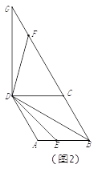
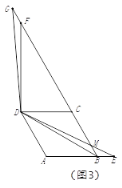
ЂкШчЭМ3ЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФбгГЄЯпЩЯЪБЃЌ
ЕФбгГЄЯпЩЯЪБЃЌ![]() НЛЩфЯп
НЛЩфЯп![]() гкЕу
гкЕу![]() ЃЛШє
ЃЛШє ![]() ,жБНгаДГіЯпЖЮ
,жБНгаДГіЯпЖЮ![]() ЕФГЄЖШ.
ЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧСтаЮЃЌЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌDHЁЭABгкЕуHЃЌСЌНгOHЃЌШєЁЯDHOЃН20ЁуЃЌдђЁЯADCЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
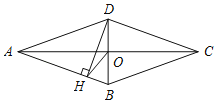
A. 120ЁуB. 130ЁуC. 140ЁуD. 150Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЃЌ
ЃЌ![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() ЗжБ№дк
ЗжБ№дк![]() ЃЌ
ЃЌ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЃЌМЧ
ЃЌМЧ![]() .
.
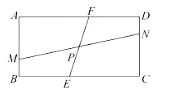
ЃЈ1ЃЉШє![]() ЕФжЕЪЧ1ЃЌЕБ
ЕФжЕЪЧ1ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ2ЃЉШє![]() ЕФжЕЪЧ
ЕФжЕЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕКЭзюаЁжЕ.
ЕФзюДѓжЕКЭзюаЁжЕ.
ЃЈ3ЃЉШє![]() ЕФжЕЪЧ3ЃЌЕБЕу
ЕФжЕЪЧ3ЃЌЕБЕу![]() ЪЧОиаЮЕФЖЅЕуЃЌ
ЪЧОиаЮЕФЖЅЕуЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com