
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
【答案】
(1)
解:∵抛物线顶点坐标为(1,﹣2),
∴可设抛物线解析式为y=a(x﹣1)2﹣2,
∵OA=3,且点A在x轴的正半轴上,
∴A(3,0),
∴0=a(3﹣1)2﹣2,解得a= ![]() ,
,
∴抛物线解析式为y= ![]() (x﹣1)2﹣2=
(x﹣1)2﹣2= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,当x=0时可得y=﹣
,当x=0时可得y=﹣ ![]() ,
,
∴B(0,﹣ ![]() ),
),
设直线AB解析式为y=kx+b,把A、B坐标代入可得 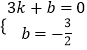 ,解得
,解得 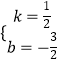 ,
,
∴y= ![]() x﹣
x﹣ ![]()
(2)
解:∵点P为线段AB上的一个动点,且PE⊥x轴,
∴点E的横坐标为x,
∵点E在抛物线上,
∴E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() )
)
(3)
解:∵点P为线段AB上的一点,
∴P(x, ![]() x﹣
x﹣ ![]() ),则E(x,
),则E(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() ),
),
∴PE= ![]() x﹣
x﹣ ![]() ﹣(
﹣( ![]() x2﹣x﹣
x2﹣x﹣ ![]() )=﹣
)=﹣ ![]() x2+
x2+ ![]() x,
x,
由(2)可知点B到PE的距离x,点A以PE的距离为3﹣x,
∴S△ABE= ![]() PEx+
PEx+ ![]() PE(3﹣x)= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/4a6d7aa9/SYS201707192035174095939404_DA/SYS201707192035174095939404_DA.001.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> PE(x+3﹣x)=
PE(3﹣x)= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/4a6d7aa9/SYS201707192035174095939404_DA/SYS201707192035174095939404_DA.001.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> PE(x+3﹣x)= ![]() PE=
PE= ![]() (﹣
(﹣ ![]() x2+
x2+ ![]() x)=﹣
x)=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当x= ![]() 时,S△ABE有最大值,最大值为
时,S△ABE有最大值,最大值为 ![]() ,
,
∴△ABE面积的最大值为 ![]()
【解析】(1)由条件可先求得抛物线解析式,则可求得B点坐标,再利用待定系数法可求得直线AB解析式;(2)由条件可知P、E的横坐标相同,又点E在抛物线上,则可表示出E点坐标;(3)由(2)可用x表示出PE的长,则可用x表示出△ABE的面积,再利用二次函数的性质可求得其最大值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE= ![]() BC,连接DE,CF.
BC,连接DE,CF. 
(1)求证:DE=CF;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象相交于点A(﹣2,1),点B(1,n).
的图象相交于点A(﹣2,1),点B(1,n). 
(1)求此一次函数和反比例函数的解析式;
(2)请直接写出满足不等式kx+b﹣ ![]() <0的解集;
<0的解集;
(3)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E(﹣a,a),如图,当曲线y= ![]() (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1 , 使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为 ![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一海伦位于灯塔P的西南方向,距离灯塔40![]() 海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=![]() (0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(﹣2,0).
(0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(﹣2,0).
(1)求k的值;
(2)直接写出阴影部分面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com