
【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE= ![]() BC,连接DE,CF.
BC,连接DE,CF. 
(1)求证:DE=CF;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
又∵F是AD的中点,∴FD= ![]() AD.
AD.
∵CE= ![]() BC,
BC,
∴FD=CE.
又∵FD∥CE,
∴四边形CEDF是平行四边形.
∴DE=CF
(2)解:过D作DG⊥CE于点G.如图所示:

∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=4,BC=AD=6.
∴∠DCE=∠B=60°.
在Rt△CDG中,∠DGC=90°,
∴∠CDG=30°,
∴CG= ![]() CD=2.
CD=2.
由勾股定理,得DG= ![]() =2
=2 ![]() .
.
∵CE= ![]() BC=3,
BC=3,
∴GE=1.
在Rt△DEG中,∠DGE=90°,
∴DE= ![]() =
= ![]() .
.
【解析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),得出四边形CEDF是平行四边形,即可得出结论;(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
【考点精析】利用平行四边形的性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我市某中学八年级一班准备在“七一”组织参加红色旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去我市龙州县红八军纪念馆参加的学生数”的扇形圆心角为60°,则下列说法中正确的是( )
A.想去龙州县红八军纪念馆参加的学生占全班学生的60%
B.想去龙州县红八军纪念馆参观的学生有12人
C.想去龙州县红八军纪念馆参观的学生肯定最多
D.想去龙州县红八军纪念馆参观的学生占全班学生的 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F. 
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,矩形ABCD关于y轴对称,点A,D在x轴上,BC交y轴于点F,E是OF的中点,抛物线y=ax2+bx+c经过B,E,C三点,已知点B(﹣2,﹣2),解答下列问题: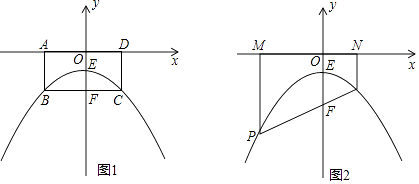
(1)填空:a= , b= , c= .
(2)如图2,这P是上述抛物线上一点,连接PF并延长交抛物线于另外一点Q,PM⊥x轴于M,QN⊥x轴于N.
①求证:PM+QN=PQ;
②若PQ=m,S四边形PMNQ= ![]() m2 , 求直线PQ对应的一次函数的解析式.
m2 , 求直线PQ对应的一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 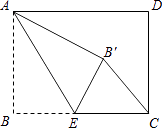
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法.如图1,在等腰△ABC中,AB=AC,AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2 , 连接AM,利用S△ABC=S△ABM+S△ACM , 可以得出结论:h=h1+h2 .
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y= ![]() x+3,l2:y=﹣3x+3,
x+3,l2:y=﹣3x+3,
若l2上一点M到l1的距离是1,试运用“阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com