
����Ŀ���Ķ����⣺���á�ͬһͼ�ε������ȡ�����֤��һЩ�����߶εĵ�ʽ���������ֽ������ķ������dz�֮Ϊ���������ͼ1���ڵ�����ABC�У�AB=AC��AC���ϵĸ�Ϊh����MΪ�ױ�BC�ϵ�����һ�㣬��M����AB��AC�ľ���ֱ�Ϊh1��h2 �� ����AM������S��ABC=S��ABM+S��ACM �� ���Եó����ۣ�h=h1+h2 ��
���̽������ͼ1�У�����M��BC���ӳ�����ʱ������h��h1��h2֮���������ϵ��֤����Ľ��ۣ�
��չӦ�ã���ͼ2����ƽ��ֱ������ϵ�У�������ֱ��l1��y= ![]() x+3��l2��y=��3x+3��
x+3��l2��y=��3x+3��
��l2��һ��M��l1�ľ�����1�������á��Ķ����⡱�͡����̽�����л�õĽ��ۣ������M�����꣮
���𰸡��⣺���̽����
���ۣ�h=h1��h2 ��
���ɣ�
��S��ABC= ![]() ACBD=
ACBD= ![]() ACh��
ACh��
S��ABM= ![]() ABME=
ABME= ![]() ABh1 ��
ABh1 ��
S��ACM= ![]() ACMF=
ACMF= ![]() ACh2 �� ��
ACh2 �� ��
�֡�S��ABC=S��ABM��S��ACM ��
�� ![]() ACh=
ACh= ![]() ABh1��
ABh1�� ![]() ACh2 ��
ACh2 ��
��AB=AC��
��h=h1��h2 ��
��չӦ�ã���y= ![]() x+3�У���x=0��y=3����y=0��x=��4��
x+3����x=0��y=3����y=0��x=��4��
��A����4��0����B��0��3����ͬ�����C��1��0����
OA=4��OB=3��AC=5��
AB= ![]() =5��
=5��
����AB=AC��
����ABC����������
���M��������x��y����
�ٵ���M��BC����ʱ����h1+h2=h�ã�
OB=1+y��y=3��1=2����������y=��3x+3����ã�x= ![]() ��
��
��M�� ![]() ��2����
��2����
�ڵ���M��CB�ӳ�����ʱ����h1��h2=h�ã�
OB=y��1��y=3+1=4����������y=��3x+3����ã�x=�� ![]() ��
��
��M���� ![]() ��4����
��4����
����������M�������� ![]() ��2����
��2���� ![]() ��4����
��4����
�����������̽�������ۣ�h=h1��h2 �� ����OA�����������������ʽ����S��ABC=S��ABM��S��ACM �� ���뻯�ɽ�����⣮
��չӦ�ã�����֤��AB=AC���������������ã�1���н��ۣ��г����̼��ɽ�����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ֻ�������Խ��Խ�ܵ����Ĺ�ע��С���ڡ�ͳ��ʵϰ��������������ѧУ������ѧ���ҳ��ԡ���ѧ�����ֻ���ѧУ������Ŀ�����ͳ�����������������µ�ͳ��ͼ�� 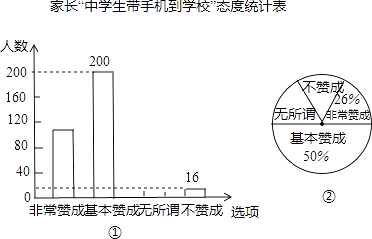
��1������ε���ļҳ��������ҳ���ʾ������ν��������������ȫͼ�٣�
��2����ͼ���б�ʾ�ҳ�������ν����Բ�ĽǵĶ�����
��3������ν��ܵ���ļҳ��У�������һ����ǡ���ǡ����ɡ�̬�ȵļҳ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��AF�۵���ʹ��D����BC�ߵĵ�E��������E��EG��CD��AF�ڵ�G������DG��
��1����֤���ı���EFDG�����Σ�
��2��̽���߶�EG��GF��AF֮���������ϵ����˵�����ɣ�
��3����AG=6��EG=2 ![]() ����BE�ij���
����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=5��BC=6������ABC�Ƶ�C˳ʱ�뷽����תһ���ǶȺ�õ���A��B��C������A��ǡ������BC���ӳ����ϣ����B�䵽BA��ľ���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE= ![]() BC������DE��CF��
BC������DE��CF�� 
��1����֤��DE=CF��
��2����AB=4��AD=6����B=60�㣬��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غϣ�չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF�������н��ۣ� �١�AGD=112.5�㣻��tan��AED= ![]() +1�����ı���AEFG�����Σ���S��ACD=
+1�����ı���AEFG�����Σ���S��ACD= ![]() S��OCD ��
S��OCD ��
������ȷ���۵������ �� ����������ȷ���۵���Ŷ����ں����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ίҪ��֯�༶��ӽ������Ϊ��ȷ��һ��ϲ���������ĸ�����Ϊÿ��س���������ί�ṩ�˴���ΪA��B��C��D���ױ�ѡ��Ŀ��ѧ��ѡ��ÿ��ѧ��ֻѡ��һ�ף�����������������ɼ������ݻ�������������������ͳ��ͼ�������ͼ1��ͼ2���ṩ����Ϣ������������⣺ 
��1���ڳ��������У���ѡ����Ŀ����ΪA��ѧ������ռ�����������İٷֱȣ�
��2���뽫ͼ2����������
��3������У����1530��ѧ�������ݳ�������Ľ��������ȫУѡ����Ŀ����ΪD��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳���Ϊ1��������ABCD��ABEF�У�����A��B��˫����y1= ![]() ��k1��0���ϣ�����E��F��˫����y2=
��k1��0���ϣ�����E��F��˫����y2= ![]() ��k2��0���ϣ�����C��D�ֱ���x���y���ϣ���k1= �� k2= ��
��k2��0���ϣ�����C��D�ֱ���x���y���ϣ���k1= �� k2= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ƹ����У�����װ��1�������2�������Һ���װ��2����������ɸ�������ЩС�����ɫ��ͬ�⣬�������ͬ�������Һ����������һ������������ĸ���Ϊ ![]() ��
��
��1�����Һ��к���ĸ�����
��2�����ȴӼ����������һ�����ٴ��Һ����������һ������������ͼ���б���������������ͬ��ɫ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com