
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为 . 
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】若记y=f(x)= ![]() ,其中f(1)表示当x=1时y的值, 即f(1)=
,其中f(1)表示当x=1时y的值, 即f(1)= ![]() =
= ![]() ;f(
;f( ![]() )表示当x=
)表示当x= ![]() 时y的值,即f(
时y的值,即f( ![]() )=
)= ![]()
![]() ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( ![]() )+f(3)+f(
)+f(3)+f( ![]() )+…+f(2011)+f(
)+…+f(2011)+f( ![]() )= .
)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)问题发现:
如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC,请判断:FG与CE的数量关系是 , 位置关系是 . 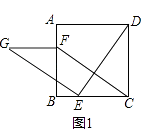
(2)拓展探究:
如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;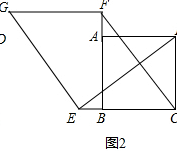
(3)类比延伸:
如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.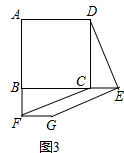
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
A.(3,0)
B.(﹣1,2)
C.(﹣3,0)
D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,矩形ABCD关于y轴对称,点A,D在x轴上,BC交y轴于点F,E是OF的中点,抛物线y=ax2+bx+c经过B,E,C三点,已知点B(﹣2,﹣2),解答下列问题: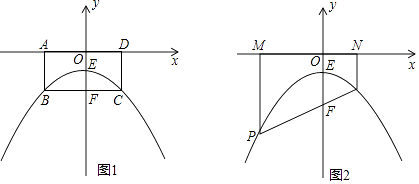
(1)填空:a= , b= , c= .
(2)如图2,这P是上述抛物线上一点,连接PF并延长交抛物线于另外一点Q,PM⊥x轴于M,QN⊥x轴于N.
①求证:PM+QN=PQ;
②若PQ=m,S四边形PMNQ= ![]() m2 , 求直线PQ对应的一次函数的解析式.
m2 , 求直线PQ对应的一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法.如图1,在等腰△ABC中,AB=AC,AC边上的高为h,点M为底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2 , 连接AM,利用S△ABC=S△ABM+S△ACM , 可以得出结论:h=h1+h2 .
类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.
拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y= ![]() x+3,l2:y=﹣3x+3,
x+3,l2:y=﹣3x+3,
若l2上一点M到l1的距离是1,试运用“阅读理解”和“类比探究”中获得的结论,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com