
【题目】计算下列各题
(1)计算:4sin60°﹣|3﹣ ![]() |+(
|+( ![]() )﹣2;
)﹣2;
(2)解方程:x2﹣ ![]() x﹣
x﹣ ![]() =0.
=0.
【答案】
(1)解:原式=2 ![]() ﹣2
﹣2 ![]() +3+4
+3+4
=7
(2)解:方法一:移项,得x2﹣ ![]() x=
x= ![]() ,
,
配方,得(x﹣ ![]() )2=1
)2=1
由此可得x﹣ ![]() =±1,
=±1,
x1=1+ ![]() ,x2=﹣1+
,x2=﹣1+ ![]()
方法二:a=1,b=﹣ ![]() ,c=﹣
,c=﹣ ![]() .
.
△=b2﹣4ac=(﹣ ![]() )2﹣4×1×(﹣
)2﹣4×1×(﹣ ![]() )=4>0
)=4>0
方程有两个不等的实数根
x= ![]() =
= ![]() =
= ![]() ±1,
±1,
x1=1+ ![]() ,x2=﹣1+
,x2=﹣1+ ![]()
【解析】(1)本题涉及负整数指数幂、二次根式化简、绝对值、特殊角的三角函数值四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;(2)利用配方法或公式法解答此题,均可得结果.
【考点精析】本题主要考查了整数指数幂的运算性质和特殊角的三角函数值的相关知识点,需要掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO. 
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y: ①求y与x之间的函数关系式;
②当BE与小圆相切时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.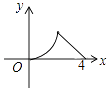
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,对角线AC的垂直平分线交AD于点E,交BC于点F,连接AF,CE,解答下列问题: 
(1)求证:四边形AECF是菱形;
(2)记AB=a,BF=b,若a,b是方程x2﹣2(m+1)x+m2+1=0的两根,问当m为何值时,菱形AECF的周长为8 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F. 
(1)求证:EF是⊙0的切线.
(2)如果⊙0的半径为5,sin∠ADE= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论: ①∠AGD=112.5°;②tan∠AED= ![]() +1;③四边形AEFG是菱形;④S△ACD=
+1;③四边形AEFG是菱形;④S△ACD= ![]() S△OCD .
S△OCD .
其中正确结论的序号是 . (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知反比例函数y= ![]() (x>0)的图象和菱形OABC,且OB=4,tan∠BOC=
(x>0)的图象和菱形OABC,且OB=4,tan∠BOC= ![]() .
. 
(1)求A、B、C三点的坐标;
(2)若将菱形向右平移,菱形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求菱形的平移距离和反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com