
【题目】如图,已知四边形ABCD是矩形,对角线AC的垂直平分线交AD于点E,交BC于点F,连接AF,CE,解答下列问题: 
(1)求证:四边形AECF是菱形;
(2)记AB=a,BF=b,若a,b是方程x2﹣2(m+1)x+m2+1=0的两根,问当m为何值时,菱形AECF的周长为8 ![]() .
.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中, 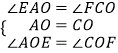 ,
,
∴△AOE≌△COF(ASA),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AECF为菱形
(2)解:在△ABF中,∵∠ABF=90°,
∴AB2+BF2=AF2,
∴AF2=a2+b2=(a+b)2﹣2ab,
由根与系数的关系得:a+b=2(m+1),ab=m2+1,
∴AF2=[2(m+1)]2﹣2(m2+1)=2m2+8m+2,
∵菱形AECF的周长为8 ![]() ,
,
∴AF=2 ![]() ,
,
∴2m2+8m+2=(2 ![]() )2,
)2,
解得:m=1或m=﹣5,
∵原方程有实数根,则△≥0,
∴[﹣2(m+1)]2﹣4(m2+1)≥0,
∴m=﹣5不合题意,舍去,
∴m=1,
即当m=1时,菱形AECF的周长为8 ![]()
【解析】(1)由ASA证明△AOE≌△COF,得出对应边相等EO=FO,证出四边形AFCE为平行四边形,再由FE⊥AC,即可得出结论.(2)由勾股定理和根与系数的关系得出方程,解方程求出m=1或m=﹣5,再由根的判别式即可得出m的值.
【考点精析】通过灵活运用根与系数的关系和线段垂直平分线的性质,掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD于点F,AD=4,EF=5,则梯形ABCD的面积是( ) 
A.40
B.30
C.20
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
①把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
②以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H. 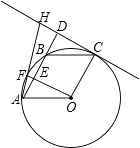
(1)求证:CD是半圆O的切线;
(2)求 ![]() 的比值;若DH=6,求EF和半径OA的长.
的比值;若DH=6,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
A.(3,0)
B.(﹣1,2)
C.(﹣3,0)
D.(﹣1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y= ![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了相应“足球进校园”的号召,某体育用品商店计划购进一批足球,第一次用6000元购进A品牌足球m个,第二次又用6000元购进B品牌足球,购进的B品牌足球的数量比购进的A品牌足球多30个,并且每个A品牌足球的进价是每个B品牌足球的进价的 ![]() .
.
(1)求m的值;
(2)若这两次购进的A,B两种品牌的足球分别按照a元/个, ![]() a元/个两种价格销售,全部销售完毕后,可获得的利润不低于4800元,求出a的最小值.
a元/个两种价格销售,全部销售完毕后,可获得的利润不低于4800元,求出a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE. 
(1)求证:BD=BC;
(2)若BD=6cm,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com