
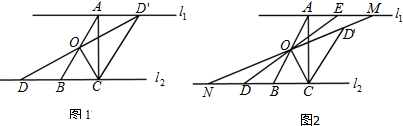
���� ��1����D����D��H��l2����ͼ1��ʾ���ɵ�DH=AC�����۵������ʼ�ƽ�Ƕ���õ���D��CH=60�㣬D��C=DC�����D��C�ij�����ΪDC�ij�������������BOCΪ�ȱ������Σ���OC����б��AB��һ�룬���BC�ij�����DC-BC���BD�ij����ɣ�
��2�����������Խ���ȵ����������Ƶõ���BOD�ס�CND�䣬�����Ƶñ����г���ϵʽ������ȷ����y��x�ĺ�������ʽ������������ɣ�
�ڹ�O��OP��BC����ͼ3��ʾ����OP�ij�����֪������DON����������DN�ij���������������ǣ�����E���߶�AM��ʱ����ͼ3��ʾ������DN�ij������AE�ij����ɣ�����E���߶�AM���ӳ�����ʱ����ͼ4��ʾ��ͬ���ɵá�BOD�ס�CND�䣬�����Ƶñ��������ʱAE�ij����ɣ�
��� �⣺��1����D����D��H��l2����ͼ1��ʾ���ɵ�DH=AC=2$\sqrt{3}$��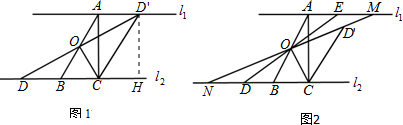
�ߡ�DCO=��D��CO=60�㣬
���D��CH=60�㣬
��CD=CD��=4��
�ߡ�DCO=��ABC=��D��CO=60�㣬
���OBCΪ�ȱ������Σ���BO=CO=BC��
��OΪRt��ABCб��AB�ϵ��е㣬
��OC=$\frac{1}{2}$AB=2����BC=2��
��BD=CD-BC=2��
��2���١ߡ�DCO=��D��CO=��BOC=60�㣬
���OBD=��NCD��=120�㣬
�ߡ�ODC=��ODC�䣬
���BOD�ס�CND�䣬
��$\frac{BO}{CN}$=$\frac{BD}{CD��}$����$\frac{2}{2+x+y}$=$\frac{x}{x+2}$��
��y=$\frac{4}{x}$-x��0��x��2����
�ڹ�O��OP��BC����ͼ3��ʾ��
��S��DON=$\frac{1}{2}$DN•OP=$\frac{3\sqrt{3}}{2}$��OP=$\sqrt{3}$��
��DN=3��
����E���߶�AM��ʱ����ͼ3��ʾ��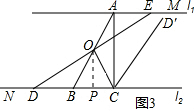
�ɵ�DN=y=3��
��$\frac{4}{x}$-x=3��
��ã�x=1����ֵ��ȥ������AE=1��
����E���߶�AM���ӳ�����ʱ����ͼ4��ʾ��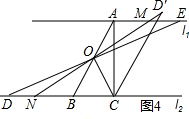
ͬ���ɵá�BOD�ס�CND�䣬
��$\frac{BO}{CN}$=$\frac{BD}{CD��}$����$\frac{2}{2+AE-3}$=$\frac{AE}{AE+2}$��
��ã�AE=4��
���ϣ�AE�ij�Ϊ1��4��
���� ���������������ۺ��⣬�漰��֪ʶ�У��ȱ������ε��ж������ʣ�ֱ��������б���ϵ��������ʣ����������ε��ж������ʣ������˷������۵�˼�룬�����������������ε��ж��������ǽⱾ��Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ��ߴ�ֱ���ı��������� | B�� | ���εĶԽ��ߴ�ֱ����� | ||
| C�� | �Խ�����ȵľ����������� | D�� | λ��ͼ��һ��������ͼ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���㷨ͳ�ڡ����й��Ŵ���ѧ�������������ҹ�������ѧ�ҳ̴�λ���ڡ��㷨ͳ�ڡ��м��أ��������⾮�����������۲�֮������4�ߣ����������۲�֮������1�ߣ�������������Σ���
���㷨ͳ�ڡ����й��Ŵ���ѧ�������������ҹ�������ѧ�ҳ̴�λ���ڡ��㷨ͳ�ڡ��м��أ��������⾮�����������۲�֮������4�ߣ����������۲�֮������1�ߣ�������������Σ���| A�� | 3��x+4��=4��x+1�� | B�� | 3x+4=4x+1 | C�� | 3��x-4��=4��x-1�� | D�� | $\frac{x}{3}-4=\frac{x}{4}-1$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com