
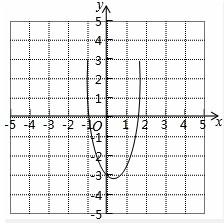
 在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
|
|
| 3 |
| 2 |
| 1 |
| 4 |
| 25 |
| 8 |
| 3 |
| 2 |
| 25 |
| 8 |
| 1 |
| 3 |
| 1 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:
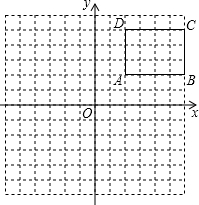 作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).
作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).查看答案和解析>>
科目:初中数学 来源: 题型:
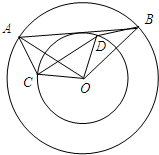 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com