
【题目】如图,EF⊥AB于F,CD⊥AB于D,点![]() 在AC边上,且∠1=∠2=
在AC边上,且∠1=∠2=![]() .
.
(1)判断DG与BC的位置关系,并加以证明;
(2)若∠AGD=![]() ,试求∠DCG的度数.
,试求∠DCG的度数.

【答案】(1)DG//BC,理由见解析;(2)∠DCG=15°.
【解析】
(1)平行,先由已知条件证明EF∥CD,所以∠2=∠DCE,又因为∠1=∠2,所以∠1=∠DCE,即可证明DG∥BC;
(2) 因为DG∥BC,根据平行线的性质得出∠AGD=∠ACB=65°,即可求出答案.
证明:(1)∵EF⊥AB于F,CD⊥AB于D,
∴∠BFE=∠BDC=90°,
∴EF∥CD;
∴∠2=∠DCE,
∵∠1=∠2,
∴∠1=∠DCE,
∴DG∥BC,
(2)解:由(1)得:DG∥BC,
∴∠AGD=∠ACB=65°,
∵EF∥CD,∠2=50°,
∴∠DCB=∠2=50°,
∴∠DCG=65°-50°=15°.


科目:初中数学 来源: 题型:
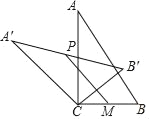
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)利用网格点画出△ABC的BC边上的高AM(点M为垂足).
(4)满足三角形ABP的面积等于三角形ACB的面积的格点P有 个(不和C重合).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为∠BAC边AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作半圆,交AC于另一点E,交AB于点F、G,连接EF.若∠BAC=22°,则∠EFG=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是腰长为1的等腰三角形,以
是腰长为1的等腰三角形,以![]() 的斜边
的斜边![]() 为直角边,画第二个等腰三角形
为直角边,画第二个等腰三角形![]() ,再以
,再以![]() 的斜边
的斜边![]() 为直角边,画第三个等腰三角形
为直角边,画第三个等腰三角形![]() ,…,以此类推,则第2019个等腰三角形的斜边长是___________。
,…,以此类推,则第2019个等腰三角形的斜边长是___________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com