练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

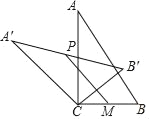
    【题目】如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最大值是_____．

    【答案】3．

    【解析】

    连接PC．先依据直角三角形斜边上中线的性质求出PC＝2，再依据三角形的三边关系可得到PM≤PC+CM，由此可得到PM的最大值为PC+CM．

    解：如图连接PC．

    在Rt△ABC中，∵∠A＝30°，BC＝2，

    ∴AB＝4，

    根据旋转不变性可知，A′B′＝AB＝4，

    ∴A′P＝PB′，

    ∴PC＝ A′B′＝2，

    ∵CM＝BM＝1，

    又∵PM≤PC+CM，即PM≤3，

    ∴PM的最大值为3（此时P、C、M共线）．

    故答案为：3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，平分，且，D为延长线上的一点，，过D作，垂足为G．下列结论：①；②；③；④，其中正确的是（　　）

    A. ①②③B. ①③④C. ①②④D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′（点B的对应点是点B'，点C的对应点是点C'），连接BB′，若AC′∥BB′，则∠C'AB′的度数为（　　）

    A. 15°B. 30°C. 45°D. 60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列条件中，①∠A+∠B=∠C； ②∠A：∠B：∠C=1：2：3； ③∠A=∠B=∠C；

    ④∠A=∠B=2∠C； ⑤∠A=2∠B=3∠C，能确定△ABC为直角三角形的条件有（　 　）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方形ABCD中，AB＝6，第1次平移将长方形ABCD沿AB的方向向右平移5个单位，得到长方形A1B1C1D1，第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位，得到长方形A2B2C2D2，…，以此类推，第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向向右平移5个单位，得到长方形AnBnCnDn（n＞2），则ABn长为 （ ）

    A. 5n＋6B. 5n＋1C. 5n＋4D. 5n＋3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题的提出：n个平面最多可以把空间分割成多少个部分？
    问题的转化：由n上面问题比较复杂，所以我们先来研究跟它类似的一个较简单的问题：
    n条直线最多可以把平面分割成多少个部分？
    如图1，很明显，平面中画出1条直线时，会得到1+1=2个部分；所以，1条直线最多可以把平面分割成2个部分；
    如图2，平面中画出第2条直线时，新增的一条直线与已知的1条直线最多有1个交点，这个交点会把新增的这条直线分成2部分，从而多出2个部分，即总共会得到1+1+2=4个部分，所以，2条直线最多可以把平面分割成4个部分；
    如图3，平面中画出第3条直线时，新增的一条直线与已知的2条直线最多有2个交点，这2个交点会把新增的这条直线分成3部分，从而多出3个部分，即总共会得到1+1+2+3=7个部分，所以，3条直线最多可以把平面分割成7个部分；
    平面中画出第4条直线时，新增的一条直线与已知的3条直线最多有3个交点，这3个交点会把新增的这条直线分成4部分，从而多出4个部分，即总共会得到1+1+2+3+4=11个部分，所以，4条直线最多可以把平面分割成11个部分；…

    （1）请你仿照前面的推导过程，写出“5条直线最多可以把平面分割成多少个部分”的推导过程（只写推导过程，不画图）；
    （2）根据递推规律用n的代数式填空：n条直线最多可以把平面分割成个部分．
    问题的解决：借助前面的研究，我们继续开头的问题；n个平面最多可以把空间分割成多少个部分？
    首先，很明显，空间中画出1个平面时，会得到1+1=2个部分；所以，1个平面最多可以把空间分割成2个部分；
    空间中有2个平面时，新增的一个平面与已知的1个平面最多有1条交线，这1条交线会把新增的这个平面最多分成2部分，从而多出2个部分，即总共会得到1+1+2=4个部分，所以，2个平面最多可以把空间分割成4个部分；
    空间中有3个平面时，新增的一个平面与已知的2个平面最多有2条交线，这2条交线会把新增的这个平面最多分成4部分，从而多出4个部分，即总共会得到1+1+2+4=8个部分，所以，3个平面最多可以把空间分割成8个部分；
    空间中有4个平面时，新增的一个平面与已知的3个平面最多有3条交线，这3条交线会把新增的这个平面最多分成7部分，从而多出7个部分，即总共会得到1+1+2+4+7=15个部分，所以，4个平面最多可以把空间分割成15个部分；
    空间中有5个平面时，新增的一个平面与已知的4个平面最多有4条交线，这4条交线会把新增的这个平面最多分成11部分，而从多出11个部分，即总共会得到1+1+2+4+7+11=26个部分，所以，5个平面最多可以把空间分割成26个部分；…
    （3）请你仿照前面的推导过程，写出“6个平面最多可以把空间分割成多少个部分？”的推导过程（只写推导过程，不画图）；
    （4）根据递推规律填写结果：10个平面最多可以把空间分割成个部分；
    （5）设n个平面最多可以把空间分割成Sn个部分，设n﹣1个平面最多可以把空间分割成Sn﹣1个部分，前面的递推规律可以用Sn﹣1和n的代数式表示Sn；这个等式是Sn= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三角形的内切圆的切点将该圆周分为5：9：10三条弧，则此三角形的最小的内角为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，回答问题
    一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20 海里的圆形区域（包括边界）都属台风区，当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里．

    （1）若这艘轮船自A处按原速度和方向继续航行，在途中会不会遇到台风？若会，试求轮船最初遇到台风的时间；若不会，说明理由；
    （2）现轮船自A处立即提高船速，向位于北偏东60°方向，相距60海里的D港驶去，为使台风到来之前，到达D港，问船速至少应提高多少（提高的船速取整数， ≈3.6）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，EF⊥AB于F，CD⊥AB于D，点在AC边上，且∠1=∠2=．

    (1)判断DG与BC的位置关系，并加以证明；

    (2)若∠AGD=，试求∠DCG的度数.

    查看答案和解析>>

    同步练习册答案