
����Ŀ���Ķ����ϣ��ش�����
һ���ִ���20����/ʱ���ٶ��������У�;�нӵ�̨�羯����̨����������40����/ʱ���ٶ��������ƶ�����̨������20 ![]() �����Բ���������߽磩����̨���������ִ���A��ʱ�����̨�������Ƶ�λ�ڵ�A���Ϸ���B������AB=100���
�����Բ���������߽磩����̨���������ִ���A��ʱ�����̨�������Ƶ�λ�ڵ�A���Ϸ���B������AB=100���
��1���������ִ���A����ԭ�ٶȺͷ���������У���;�л������̨�磿���ᣬ�����ִ��������̨���ʱ�䣻�����ᣬ˵�����ɣ�
��2�����ִ���A��������ߴ��٣���λ�ڱ�ƫ��60�㷽�����60�����D��ʻȥ��Ϊʹ̨�絽��֮ǰ������D�ۣ��ʴ�������Ӧ��߶��٣���ߵĴ���ȡ������ ![]() ��3.6����
��3.6����
���𰸡�
��1���⣺��;�л�����̨�磬���������̨���ʱ��ΪtСʱ����ʱ���ִ�λ��C����̨�������Ƶ�E�������У�
AC=20t��AE=AB��BE=100��40t��EC=20 ![]() ��
��
��Rt��AEC��AC2+AE2=EC2��
��20t��2+��100��40t��2=��20 ![]() ��2��
��2��
�����ã�t2��4t+3=0��
��ã�t1=1��t2=3��
���ԣ�;�н�����̨�磬�������̨���ʱ��Ϊ1Сʱ
��2���⣺��̨��ִ�D��ΪtСʱ����ʱ̨��������M�㣬��D��DF��AB������ΪF��
����DM��

��Rt��ADF�У�AD=60����FAD=60�㣬
��DF=30 ![]() ��FA=30��
��FA=30��
��FM=FA+AB��BM=130��40t��MD=20 ![]() ��
��
�ࣨ30 ![]() ��2+��130��40t��2=��20
��2+��130��40t��2=��20 ![]() ��2��
��2��
�����ã�4t2��26t+39=0��
��ã�t1= ![]() ��t2=
��t2= ![]() ��
��
��̨��ִ�D��ʱ��Ϊ�� ![]() Сʱ��
Сʱ��
���ִ���A���� ![]() Сʱ����D�ۣ����ٶ�Ϊ��60��
Сʱ����D�ۣ����ٶ�Ϊ��60�� ![]() ��25.5��
��25.5��
��Ϊʹ̨��ִ�D��֮ǰ�ִ�����D�ۣ��ִ�����Ӧ����6����/ʱ��
��������1�����ȱ�ʾ��AC=20t��AE=AB-BE=100-40t�������ù��ɶ����ó�t��ֵ�������ó��𰸣�
��2��ֱ�ӱ�ʾ��FM=FA+AB-BM=130-40t��MD=20 ![]() �������ù��ɶ����ó��𰸣�
�������ù��ɶ����ó��𰸣�
�����㾫����������Ҫ�����˹��ɶ����ĸ�����ڷ������������֪ʶ�㣬��Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��ָ����ָ�Ϸ�������Ŀ�귽�� �����ɵ�С��90���ˮƽ�ǣ���������Dz�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ���AC���е�O��EF��AC����BC���ڵ�E����AD���ڵ�F���ֱ�����AE��CF����AB=2 ![]() ����DCF=30�㣬��EF�ij�Ϊ�� ��
����DCF=30�㣬��EF�ij�Ϊ�� ��
A.4
B.6
C.![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������ABC�ƶ���C��ʱ����ת�õ���A��B��C��M��BC���е㣬P��A��B�����е㣬����PM����BC��2����BAC��30�������߶�PM�����ֵ��_____��
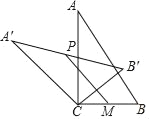
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������O��BC��D����D����O������DE��AC��E����DE��AC�������������������Ƴ�����ȷ�����У���Ҫ���ٱ�ע������ĸ���ҽ��۵Ĺ��������������߲��ܳ����ڽ����У���д�������̣�����д��4�����ۣ����۲�����ͬ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ľ�ƽ����BD��CE�ཻ�ڵ�P.
��1�������A=70��������BPC�Ķ�����
��2����ͼ������P����ֱ��MN��BC���ֱ�AB��AC�ڵ�M��N��������MPB+��NPC�Ķ������ú���A�Ĵ���ʽ��ʾ����
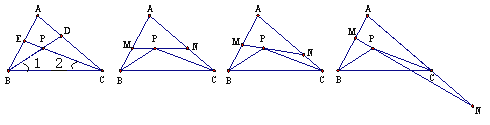
�� �� �� ��
�ڣ�2���������£���ֱ��MN�Ƶ�P��ת.
��������ֱ��MN��AB��AC�Ľ����Էֱ����߶�AB��AC��ʱ����ͼ������̽����MPB����NPC����A����֮���������ϵ����˵��������ɣ�
��������ֱ��MN��AB�Ľ��������߶�AB�ϣ�����AC�Ľ�����AC���ӳ�����ʱ����ͼ�������ʣ���������MPB����NPC����A����֮���������ϵ�Ƿ���Ȼ����������������˵��������ɣ������������������MPB����NPC����A����֮���������ϵ����˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������㴫ͳ�Ļ���ijУΪ�����![]() ��������
��������![]() ��
��![]() ˮ䰴�
ˮ䰴�![]() ע�����������ף�����ÿ��
ע�����������ף�����ÿ��![]() ��������
��������![]() ע�������ļ۸��ÿ��
ע�������ļ۸��ÿ��![]() ˮ䰴�
ˮ䰴�![]() ע�������ļ۸��60Ԫ����4800Ԫ����
ע�������ļ۸��60Ԫ����4800Ԫ����![]() ˮ䰴�
ˮ䰴�![]() ע����������������3600Ԫ����
ע����������������3600Ԫ����![]() ��������
��������![]() ע������������2������ÿ��
ע������������2������ÿ��![]() ˮ䰴�
ˮ䰴�![]() ע�������ļ۸�
ע�������ļ۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ��12�׳���ľ������һ����һ���ᵲ�ľ��δ�������ͼ����������ƴ��ڵĸߺͿ��ij��ȣ�����ʹ����������Ĺ�����࣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�DZ߳�3cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��Ϊt��s����������⣺��tΪ��ֵʱ����PBQ��ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����3��2����B��0��4����C��0��2����
��1������ABC�Ե�CΪ��ת������ת180����������ת���Ӧ����A1B1C1��ƽ����ABC������A�Ķ�Ӧ��A2������Ϊ��0����4��������ƽ�ƺ��Ӧ����A2B2C2��
��2��������A1B1C1��ijһ����ת���Եõ���A2B2C2����ֱ��д����ת���ĵ����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com