
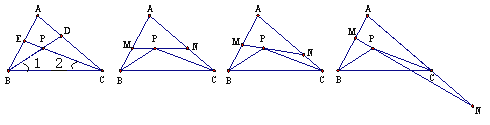
【题目】如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,过P点作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示);
① ② ③ ④
在(2)的条件下,将直线MN绕点P旋转.
(ⅰ)当直线MN与AB、AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
【答案】(1)125°;(2)∠MPB+∠NPC=90°-![]() ∠A;(3)∠MPB+∠NPC= 90°-
∠A;(3)∠MPB+∠NPC= 90°-![]() ∠A,∠MPB-∠NPC=90°-
∠A,∠MPB-∠NPC=90°-![]() ∠A.
∠A.
【解析】
试题(1)由三角形内角和定理可知∠ABC+∠ACB=180°-∠A,由角平分线的性质可知及三角形内角和定理可求出∠BPC的度数;
(2)利用平行线的性质求解或先说明∠BPC=90°+![]() ∠A;
∠A;
(3)(ⅰ)先说明∠BPC=90°+![]() ∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-
∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-![]() ∠A.理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+
∠A.理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+![]() ∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+
∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A.
∠A.
试题解析::(1)∵在△ABC中,∠A+∠B+∠ACB=180°,
∵∠A=70°,
∴∠ABC+∠ACB=110°,
∵∠1=![]() ∠ABC,
∠ABC,
∠2=![]() ∠ACB,
∠ACB,
∴∠1+∠2=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=![]() ×110°=55°,
×110°=55°,
∴∠BPC=180°-(∠1+∠2)=180°-55°=125°;
(2)由(1)可证∠BPC=90°+![]() ∠A,
∠A,
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)=90°-
∠A)=90°-![]() ∠A;
∠A;
(3)(ⅰ)∠MPB+∠NPC= 90°-![]() ∠A.
∠A.
理由:先说明∠BPC=90°+![]() ∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A;
∠A;
(ⅱ)不成立(1分),∠MPB-∠NPC=90°-![]() ∠A(1分).
∠A(1分).
理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+![]() ∠A,
∠A,
∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A.
∠A.
考点: (1)平行线的性质;2.角平分线的性质;3.三角形内角和.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
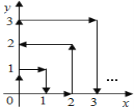
【题目】如图,一只跳蚤在第一象限及x轴、y轴上跳动,第一秒它从原点跳动到点(0,1),第二秒它从点(0,1)跳到点(1,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳动一个单位长度,那么30秒后跳蚤所在位置的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2,…,以此类推,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向向右平移5个单位,得到长方形AnBnCnDn(n>2),则ABn长为 ( )

A. 5n+6B. 5n+1C. 5n+4D. 5n+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20 ![]() 海里的圆形区域(包括边界)都属台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.
海里的圆形区域(包括边界)都属台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.
(1)若这艘轮船自A处按原速度和方向继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,说明理由;
(2)现轮船自A处立即提高船速,向位于北偏东60°方向,相距60海里的D港驶去,为使台风到来之前,到达D港,问船速至少应提高多少(提高的船速取整数, ![]() ≈3.6)?
≈3.6)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com