练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

    （1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；

    （2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．

    【答案】（1）图形见解析；（2）P点坐标为（，﹣1）．

    【解析】

    （1）分别作出点A、B关于点C的对称点，再顺次连接可得；由点A的对称点A2的位置得出平移方向和距离，据此作出另外两个点的对应点，顺次连接可得；
    （2）连接A1A2、B1B2，交点即为所求．

    （1）如图所示：A1（3，2）、C1（0，2）、B1（0，0）；A2（0，-4）、B2（3，﹣2）、C2（3，﹣4）．

    （2）将△A1B1C1绕某一点旋转可以得到△A2B2C2，旋转中心的P点坐标为（，﹣1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料，回答问题
    一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20 海里的圆形区域（包括边界）都属台风区，当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里．

    （1）若这艘轮船自A处按原速度和方向继续航行，在途中会不会遇到台风？若会，试求轮船最初遇到台风的时间；若不会，说明理由；
    （2）现轮船自A处立即提高船速，向位于北偏东60°方向，相距60海里的D港驶去，为使台风到来之前，到达D港，问船速至少应提高多少（提高的船速取整数， ≈3.6）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，EF⊥AB于F，CD⊥AB于D，点在AC边上，且∠1=∠2=．

    (1)判断DG与BC的位置关系，并加以证明；

    (2)若∠AGD=，试求∠DCG的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（生活常识）

    射到平面镜上的光线（入射光线）和变向后的光线（反射光线）与平面镜所夹的角相等。如图 1，MN 是平面镜，若入射光线 AO 与水平镜面夹角为∠1，反射光线 OB 与水平镜面夹角为∠2，则∠1=∠2 .

    （现象解释）

    如图 2，有两块平面镜 OM，ON，且 OM⊥ON，入射光线 AB 经过两次反射，得到反射光线 CD.求证 AB∥CD.

    （尝试探究）

    如图 3，有两块平面镜 OM，ON，且∠MON =55 ，入射光线 AB 经过两次反射，得到反射光线 CD，光线 AB 与 CD 相交于点 E，求∠BEC 的大小.

    （深入思考）

    如图 4，有两块平面镜 OM，ON，且∠MON α ，入射光线 AB 经过两次反射，得到反射光线 CD，光线 AB 与 CD 所在的直线相交于点 E，∠BED=β , α 与 β 之间满足的等量关系是 .（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有（　 ）

    ①AM∥BN；②AM=BN；③BC=ML；④∠ACB=∠MNL。

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地区为了进一步缓解交通拥堵问题，决定修建一条长为7千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）在30≤x≤12 0之间时具有一次函数的关系，如下表所示．

    x

    50

    60

    90

    120

    y

    40

    38

    32

    26


    （1）求y关于x的函数关系式；
    （2）后来在修建的过程中计划发生改变，政府决定多修3千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+2的图象与x轴交于点A（﹣1，0）、B（4，0），与y轴交于点C．

    （1）a=；b=；
    （2）点P为该函数在第一象限内的图象上的一点，过点P作PQ⊥BC于点Q，连接PC．
    ①求线段PQ的最大值；
    ②若以P、C、Q为顶点的三角形与△ABC相似，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AC=9，BC=12，在Rt△DEF中，∠DFE=90°，EF=6，DF=8，E、F两点在BC边上，DE、DF两边分别与AB边交于点G、H．固定△ABC不动，△DEF从点F与点B重合的位置出发，沿BC边以每秒1个单位的速度向点C运动；同时点P从点F出发，在折线FD﹣DE上以每秒2个单位的速度向点E运动．当点E到达点C时，△DEF和点P同时停止运动．设运动时间为t（秒）．

    （1）当t=2时，PH=cm，DG=cm；
    （2）当t为何值时，△PDG为等腰三角形？请说明理由；
    （3）当t为何值时，点P与点G重合？写出计算过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图①、图②是8×5的正方形网格，线段AB、BC的端点均在格点上．按要求在图①、图②中以AB、BC为邻边各画一个四边形ABCD，使点D在格点上．要求所画两个四边形不全等，且同时满足四边形ABCD是轴对称图形，点D到∠ABC两边的距离相等．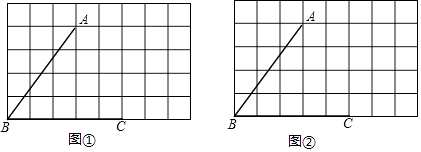

    查看答案和解析>>

    同步练习册答案