
【题目】(生活常识)
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等。如图 1,MN 是平面镜,若入射光线 AO 与水平镜面夹角为∠1,反射光线 OB 与水平镜面夹角为∠2,则∠1=∠2 .

(现象解释)
如图 2,有两块平面镜 OM,ON,且 OM⊥ON,入射光线 AB 经过两次反射,得到反射光线 CD.求证 AB∥CD.
(尝试探究)
如图 3,有两块平面镜 OM,ON,且∠MON =55 ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 相交于点 E,求∠BEC 的大小.

(深入思考)
如图 4,有两块平面镜 OM,ON,且∠MON α ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 所在的直线相交于点 E,∠BED=β , α 与 β 之间满足的等量关系是 .(直接写出结果)
【答案】【现象解释】见解析;【尝试探究】BEC 70;【深入思考】 2.
【解析】
[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠3+∠4=180°,即可得出∠DCB+∠ABC=180°,即可证得AB∥CD;
[尝试探究]根据三角形内角和定理求得∠2+∠3=125°,根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用平角的定义得出∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,即可得出∠EBC+BCE=360°-250°=110°,根据三角形内角和定理即可得出∠BEC=180°-110°=70°;
[深入思考]利用平角的定义得出∠ABC=180°-2∠2,∠BCD=180°-2∠3,利用外角的性质∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,而∠BOC=∠3-∠2=α,即可证得β=2α.
[现象解释]
如图2,
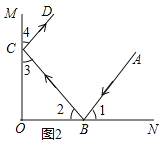
∵OM⊥ON,
∴∠CON=90°,
∴∠2+∠3=90°
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=180°,
∴∠DCB+∠ABC=180°,
∴AB∥CD;
【尝试探究】
如图3,
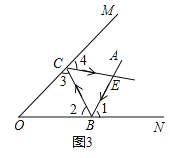
在△OBC中,∵∠COB=55°,
∴∠2+∠3=125°,
∵∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=250°,
∵∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,
∴∠EBC+BCE=360°-250°=110°,
∴∠BEC=180°-110°=70°;
【深入思考】
如图4,
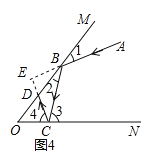
β=2α,
理由如下:∵∠1=∠2,∠3=∠4,
∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,
∴∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,
∵∠BOC=∠3-∠2=α,
∴β=2α.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)利用网格点画出△ABC的BC边上的高AM(点M为垂足).
(4)满足三角形ABP的面积等于三角形ACB的面积的格点P有 个(不和C重合).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为∠BAC边AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作半圆,交AC于另一点E,交AB于点F、G,连接EF.若∠BAC=22°,则∠EFG=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).

请你根据图中所给的信息解答下列问题:
(1)请将两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_____人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积. 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com