
【题目】如图,点D为∠BAC边AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作半圆,交AC于另一点E,交AB于点F、G,连接EF.若∠BAC=22°,则∠EFG=°.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,EF⊥AB于F,CD⊥AB于D,点![]() 在AC边上,且∠1=∠2=
在AC边上,且∠1=∠2=![]() .
.
(1)判断DG与BC的位置关系,并加以证明;
(2)若∠AGD=![]() ,试求∠DCG的度数.
,试求∠DCG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一副三角板按如图拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转一个大小为![]() 的角(
的角(![]() )得三角形ABC′如图所示.
)得三角形ABC′如图所示.

试问:(1)当旋转到如图的位置时,则![]() = °;
= °;

(2)当![]() = °时,能使如图中3的AB//CD;
= °时,能使如图中3的AB//CD;
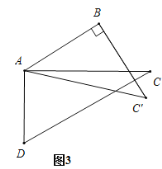
(3)连接BD,当![]() 时,探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的说明.
时,探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(生活常识)
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等。如图 1,MN 是平面镜,若入射光线 AO 与水平镜面夹角为∠1,反射光线 OB 与水平镜面夹角为∠2,则∠1=∠2 .

(现象解释)
如图 2,有两块平面镜 OM,ON,且 OM⊥ON,入射光线 AB 经过两次反射,得到反射光线 CD.求证 AB∥CD.
(尝试探究)
如图 3,有两块平面镜 OM,ON,且∠MON =55 ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 相交于点 E,求∠BEC 的大小.

(深入思考)
如图 4,有两块平面镜 OM,ON,且∠MON α ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 所在的直线相交于点 E,∠BED=β , α 与 β 之间满足的等量关系是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2的图象与x轴交于点A(﹣1,0)、B(4,0),与y轴交于点C.
(1)a=;b=;
(2)点P为该函数在第一象限内的图象上的一点,过点P作PQ⊥BC于点Q,连接PC.
①求线段PQ的最大值;
②若以P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以边AB上的一点O为圆心,以OA的长为半径的圆交边AB于点D,BC与⊙O相切于点C.若⊙O的半径为5,∠A=20°,则 ![]() 的长为 .
的长为 . 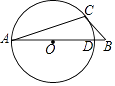
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com