
【题目】问题的提出:n个平面最多可以把空间分割成多少个部分?
问题的转化:由n上面问题比较复杂,所以我们先来研究跟它类似的一个较简单的问题:
n条直线最多可以把平面分割成多少个部分?
如图1,很明显,平面中画出1条直线时,会得到1+1=2个部分;所以,1条直线最多可以把平面分割成2个部分;
如图2,平面中画出第2条直线时,新增的一条直线与已知的1条直线最多有1个交点,这个交点会把新增的这条直线分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2条直线最多可以把平面分割成4个部分;
如图3,平面中画出第3条直线时,新增的一条直线与已知的2条直线最多有2个交点,这2个交点会把新增的这条直线分成3部分,从而多出3个部分,即总共会得到1+1+2+3=7个部分,所以,3条直线最多可以把平面分割成7个部分;
平面中画出第4条直线时,新增的一条直线与已知的3条直线最多有3个交点,这3个交点会把新增的这条直线分成4部分,从而多出4个部分,即总共会得到1+1+2+3+4=11个部分,所以,4条直线最多可以把平面分割成11个部分;…
(1)请你仿照前面的推导过程,写出“5条直线最多可以把平面分割成多少个部分”的推导过程(只写推导过程,不画图);
(2)根据递推规律用n的代数式填空:n条直线最多可以把平面分割成个部分.
问题的解决:借助前面的研究,我们继续开头的问题;n个平面最多可以把空间分割成多少个部分?
首先,很明显,空间中画出1个平面时,会得到1+1=2个部分;所以,1个平面最多可以把空间分割成2个部分;
空间中有2个平面时,新增的一个平面与已知的1个平面最多有1条交线,这1条交线会把新增的这个平面最多分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2个平面最多可以把空间分割成4个部分;
空间中有3个平面时,新增的一个平面与已知的2个平面最多有2条交线,这2条交线会把新增的这个平面最多分成4部分,从而多出4个部分,即总共会得到1+1+2+4=8个部分,所以,3个平面最多可以把空间分割成8个部分;
空间中有4个平面时,新增的一个平面与已知的3个平面最多有3条交线,这3条交线会把新增的这个平面最多分成7部分,从而多出7个部分,即总共会得到1+1+2+4+7=15个部分,所以,4个平面最多可以把空间分割成15个部分;
空间中有5个平面时,新增的一个平面与已知的4个平面最多有4条交线,这4条交线会把新增的这个平面最多分成11部分,而从多出11个部分,即总共会得到1+1+2+4+7+11=26个部分,所以,5个平面最多可以把空间分割成26个部分;…
(3)请你仿照前面的推导过程,写出“6个平面最多可以把空间分割成多少个部分?”的推导过程(只写推导过程,不画图);
(4)根据递推规律填写结果:10个平面最多可以把空间分割成个部分;
(5)设n个平面最多可以把空间分割成Sn个部分,设n﹣1个平面最多可以把空间分割成Sn﹣1个部分,前面的递推规律可以用Sn﹣1和n的代数式表示Sn;这个等式是Sn= .
【答案】
(1)解:根据规律得,平面中画出第5条直线时,新增的一条直线与已知的4条直线最多有4个交点,这4个交点会把新增的这条直线分成5部分,从而多出5个部分,即总共会得到1+1+2+3+4+5=16个部分,所以,5条直线最多可以把平面分割成16个部分
(2)1+ ![]()
(3)解:根据规律得,空间中有6个平面时,新增的一个平面与已知的5个平面最多有5条交线,这5条交线会把新增的这个平面最多分成16部分,而从多出16个部分,即总共会得到1+1+2+4+7+11+16=42个部分,所以,6个平面最多可以把空间分割成42个部分
(4)176
(5)Sn﹣1+[1+ ![]() ]
]
【解析】解:(2)根据规律得,n条直线最多可以把平面分割成1+1+2+3+4+…+n=1+ ![]() ,
,
所以答案是1+ ![]() ;
;
⑷根据规律得,空间中有10个平面时,新增的一个平面与已知的9个平面最多有9条交线,这9条交线会把新增的这个平面最多分成37部分,而从多出37个部分,即总共会得到1+1+2+4+7+11+16+…+37=176个部分,所以,10个平面最多可以把空间分割成176个部分;
所以答案是:176;
⑸根据规律得,空间中有n个平面时,新增的一个平面与已知的(n﹣1)个平面最多有(n﹣1)条交线,这(n﹣1)条交线会把新增的这个平面最多分成[1+ ![]() ]部分,
]部分,
∴Sn=Sn﹣1+[1+ ![]() ]
]
所以答案是:Sn﹣1+[1+ ![]() ].
].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格纸中,点A、B、C在小正方形的顶点上.
(1)求![]() 的面积;
的面积;
(2)在图中画出与![]() 关于直线1成轴对称的
关于直线1成轴对称的![]() ;
;
(3)在如图所示网格纸中,以![]() 为一边作与
为一边作与![]() 全等的三角形,可以作出多少个三角形与
全等的三角形,可以作出多少个三角形与![]() 全等(不要超出网格纸的范围).
全等(不要超出网格纸的范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款产品,成本价为每件10元.投放市场进行试销,得到如下数据:
售价x(元/件) | … | 30 | 40 | 50 | 60 | … |
日销售量y(件) | … | 50 | 40 | 30 | 20 | … |
(1)若日销售量y(件)是售价x(元/件)的一次函数,求这个一次函数解析式.
(2)设这个工厂试销该产品每天获得的利润为w(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?(每天利润=每天销售总收入﹣每天销售总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2.请用面积法证明:h1+h2=h;

(2)当点M在BC延长线上时,h1、h2、h之间的等量关系式是 ;(直接写出结论不必证明)
(3)如图2在平面直角坐标系中有两条直线l1:y=![]() x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
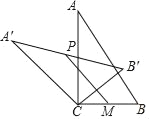
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角梯形的一个内角为120°,较长的腰为6cm,有一底边长为5cm,则这个梯形的面积为( )
A.![]() cm2
cm2
B.![]() cm2
cm2
C.25 ![]() cm2
cm2
D.![]() cm2或
cm2或 ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传承优秀传统文化,某校为各班购进![]() 三国演义
三国演义![]() 和
和![]() 水浒传
水浒传![]() 注音读本若干套,其中每套
注音读本若干套,其中每套![]() 三国演义
三国演义![]() 注音读本的价格比每套
注音读本的价格比每套![]() 水浒传
水浒传![]() 注音读本的价格贵60元,用4800元购买
注音读本的价格贵60元,用4800元购买![]() 水浒传
水浒传![]() 注音读本的套数是用3600元购买
注音读本的套数是用3600元购买![]() 三国演义
三国演义![]() 注音读本套数的2倍,求每套
注音读本套数的2倍,求每套![]() 水浒传
水浒传![]() 注音读本的价格.
注音读本的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)利用网格点画出△ABC的BC边上的高AM(点M为垂足).
(4)满足三角形ABP的面积等于三角形ACB的面积的格点P有 个(不和C重合).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com