
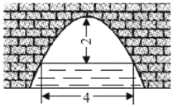
【题目】如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面![]() 为4米,则当水面下降1米时,水面宽度增加__________米.
为4米,则当水面下降1米时,水面宽度增加__________米.
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测.根据检测结果,制成下面不完整的统计图表.
被抽样的学生视力情况频数表
组别 | 视力段 | 频数 |
A | 5.1≤x≤5.3 | 25 |
B | 4.8≤x≤5.0 | 115 |
C | 4.4≤x≤4.7 | m |
D | 4.0≤x≤4.3 | 52 |
(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数.根据上述图表信息,你对视力保护有什么建议?

查看答案和解析>>
科目:初中数学 来源: 题型:
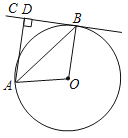
【题目】如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6cm时.
①直接写出扇形AOB的面积约为 cm2(结果精确到1cm2);
②点E是⊙O上一动点(点E不与点A、点B重合),连接AE,BE,请直接写出∠AEB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上.
轴的正半轴上.
(1)分别以点![]() ,
,![]() ,
,![]() 为圆心,
为圆心,![]() 为半径作圆,得到
为半径作圆,得到![]() ,
,![]() 和
和![]() ,其中是
,其中是![]() 的角内圆的是_______;
的角内圆的是_______;
(2)如果以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 为
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(3)点![]() 在第一象限内,如果存在一个半径为
在第一象限内,如果存在一个半径为![]() 且过点
且过点![]() 的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多![]() 元,用
元,用![]() 元购买的跳绳个数和用
元购买的跳绳个数和用![]() 元购买的子数量相同.
元购买的子数量相同.
(1)求跳绳和毯子的单价分别是多少元?
(2)学校计划购买跳绳和毯子两种器材共![]() 个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的
个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的![]() 倍,跳绳的数量不多于
倍,跳绳的数量不多于![]() 根,请你求出学校花钱最少的购买方案.
根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
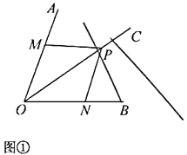
【题目】问题呈现:下图是小明复习全等三角形时遇到的一个问题并引发的思考,请帮助小明完成以下学习任务.

请根据小明的思路,结合图①,写出完整的证明过程.结论应用:
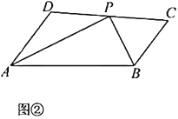
(1)如图②,在四边形![]() 中,
中,![]() ,
,![]() 的平分线和
的平分线和![]() 的平分线交于
的平分线交于![]() 边上点
边上点![]() .求证:
.求证:![]() ;
;
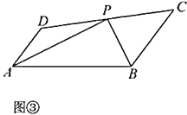
(2)在(1)的条件下,如图③,若![]() ,
,![]() .当
.当![]() 有一个内角是
有一个内角是![]() 时,
时,![]() 的面积是 .
的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的两条对角线相交于点
的两条对角线相交于点![]() 轴,垂足为点
轴,垂足为点![]() 正比例函数
正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 两点.
两点.

(1)求正比例函数和反比例函数的解析式;
(2)求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com