
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上.
轴的正半轴上.
(1)分别以点![]() ,
,![]() ,
,![]() 为圆心,
为圆心,![]() 为半径作圆,得到
为半径作圆,得到![]() ,
,![]() 和
和![]() ,其中是
,其中是![]() 的角内圆的是_______;
的角内圆的是_______;
(2)如果以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 为
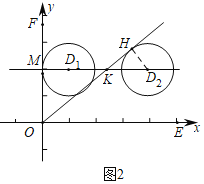
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(3)点![]() 在第一象限内,如果存在一个半径为
在第一象限内,如果存在一个半径为![]() 且过点
且过点![]() 的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)画出图象,根据角内相切圆的定义判断即可;
(2)求出两种特殊位置时t的值即可判断;
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,![]() )的圆为∠EOM的角内相切圆.
)的圆为∠EOM的角内相切圆.
(1)如图1中,
∵点A(1,0),B(1,1),C(3,2)
∴观察图象可知,⊙B和⊙C是∠EOF的角内圆.

(2)当![]() 与
与![]() 轴相切时,设切点为
轴相切时,设切点为![]() ,则
,则![]() ,可得
,可得![]() .
.
当![]() 与
与![]() 相切时,设切点为
相切时,设切点为![]() ,连接
,连接![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,
则![]() ,
,![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
可得![]() ,可知,满足条件的
,可知,满足条件的![]() 的取值范围是
的取值范围是![]() .
.
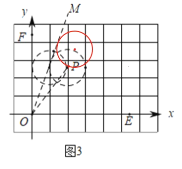
(3)如图3中,连接OP,OM.
∵点P(2,![]() ),
),
∴tan∠POE=![]() =
=![]()
∴∠POE=60°,
观察图象可知,当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,
存在一个半径为1且过点点P(2,![]() )的圆为∠EOM的角内相切圆,
)的圆为∠EOM的角内相切圆,
∴60°≤∠EOM<90°.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
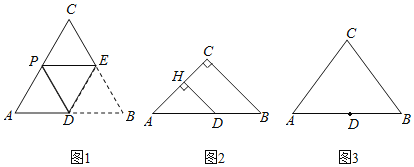
【题目】已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=![]() AC;
AC;
(2)变式求异 如图2,若∠C=90°,m=6![]() ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
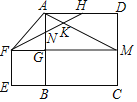
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至E使
至E使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于M,连接
于M,连接![]() ,
,![]() ,H为
,H为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点N、K.则下列结论:
交于点N、K.则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的是______________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
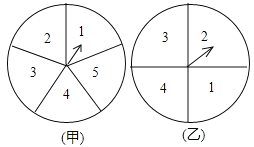
【题目】小明和小亮用如图所示的甲、乙两个转盘(甲转盘被分成五个面积相等的扇形,乙转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次(如果指针恰好在分割线上,那么重转一次,直到指针指向某一扇形区域为止).
(1)请你求出甲转盘指针指向偶数区域的概率;
(2)若两次数字之和为![]() ,
,![]() 或
或![]() 时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组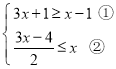 ,请结合题意填空,完成本题的解答.
,请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
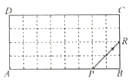
【题目】如图,在矩形![]() 中,
中,![]() ,一发光电子开始置于
,一发光电子开始置于![]() 边的点
边的点![]() 处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着
处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着![]() 方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于
方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于![]() ,当发光电子与矩形的边碰撞2020次后,它与
,当发光电子与矩形的边碰撞2020次后,它与![]() 边的碰撞次数是__________.
边的碰撞次数是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com