

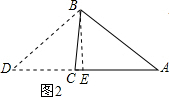
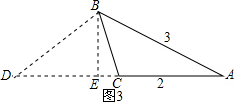
 解:(1)如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,则BE是中垂线,
解:(1)如图2,作BE⊥AC于点E,在AC的延长线上取点D,使得DE=AE,连接BD,则BE是中垂线,| 1 |
| 2 |
| 1 |
| 2 |
| b+c |
| 2 |
| b+c |
| 2 |
| c-b |
| 2 |
| c-b |
| 2 |
| b+c |
| 2 |
| c2-a2 |
| c |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |


科目:初中数学 来源: 题型:
 小彬的爸爸制作了一件边框为长方形的工艺品,挂在墙上很漂亮,但小彬看来看去总觉得它不像长方形,经过思考小彬仅用一把刻度尺(尺的长度足够)就解决了问题,你能说出他用的是什么方法吗?(简要说明一下操作过程及相关理由)
小彬的爸爸制作了一件边框为长方形的工艺品,挂在墙上很漂亮,但小彬看来看去总觉得它不像长方形,经过思考小彬仅用一把刻度尺(尺的长度足够)就解决了问题,你能说出他用的是什么方法吗?(简要说明一下操作过程及相关理由)查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间x(小时) | 划记 | 人数 | 所占百分比 |
| 0.5x≤x≤1.0 | 正正 | 14 | 28% |
| 1.0≤x<1.5 | 正正正 | 15 | 30% |
| 1.5≤x<2 |  | 7 | |
| 2≤x<2.5 | 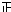 | 4 | 8% |
| 2.5≤x<3 | 正 | 5 | 10% |
| 3≤x<3.5 | 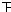 | 3 | |
| 3.5≤x<4 | 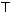 | 4% | |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、∠A=∠C-∠B | ||||
| B、a2=c2-b2 | ||||
C、a=k,b=
| ||||
| D、a:b:c=2:3:4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com