
 如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积.
如图,M是?ABCD的AB边的中点,CM与BD相交于点E,连接DM,设?ABCD的面积为1,求图中阴影部分的面积. 分析 平行四边形的面积为1,则△DAM的面积=$\frac{1}{2}$S△DAB=$\frac{1}{4}$S?ABCD,由于$\frac{BE}{DE}$=$\frac{MB}{CD}$=$\frac{1}{2}$,所以△EMB上的高线与△DAB上的高线比为$\frac{BE}{BD}$=$\frac{1}{3}$,所以S△EMB=$\frac{1}{3}$×$\frac{1}{2}$S△DAB=$\frac{1}{12}$,于是S△DEC=4S△MEB=$\frac{1}{3}$,由此可以求出阴影面积,从而求出面积比为$\frac{1}{3}$,代入求出即可.
解答 解:设平行四边形的面积为1,
∵四边形ABCD是平行四边形,
∴S△DAB=$\frac{1}{2}$S?ABCD,
又∵M是?ABCD的AB的中点,
则S△DAM=$\frac{1}{2}$S△DAB=$\frac{1}{4}$S?ABCD,
∵$\frac{BE}{DE}$=$\frac{MB}{CD}$=$\frac{1}{2}$,
∴△EMB上的高线与△DAB上的高线比为=$\frac{BE}{BD}$=$\frac{1}{3}$,
∴S△EMB=$\frac{1}{3}$×$\frac{1}{2}$S△DAB=$\frac{1}{12}$,
∴S△DEC=4S△MEB=$\frac{1}{3}$,
S阴影面积=1-$\frac{1}{4}$-$\frac{1}{12}$-$\frac{1}{3}$=$\frac{1}{3}$,
即图中阴影部分的面积是$\frac{1}{3}$.
点评 此题主要考查平行四边形的性质和相似比的内容,能正确运用知识点求出各个部分的面积是解此题的关键,比较复杂,有一定的综合性.


科目:初中数学 来源: 题型:选择题
| A. | 检测天津市的空气质量 | |
| B. | 了解我市中学生的体育锻炼情况 | |
| C. | 滨海新区招聘,对应聘人员进行面试 | |
| D. | 调查我市居民对于禁烟条例的支持度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
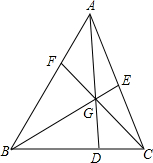 如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC.
如图,在三角形ABC中,点D,E,F分别在BC,AC,AB上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,若S△BDG=8,S△AGE=3,求S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
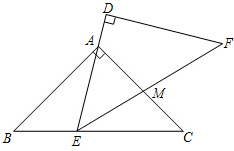 如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2;
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=$\sqrt{2}$.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC=2;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
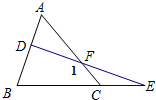 如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )| A. | ∠A+∠B=∠1+∠E | B. | ∠A+∠B=∠1-∠E | C. | ∠A-∠B=∠1-∠E | D. | ∠A-∠B=∠1+∠E |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com