
【题目】如图,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,从而把AB,AD,DC转化在一个三角形中即可判断.试探究AB,AD,DC之间的等量关系,并证明你的结论.
科目:初中数学 来源: 题型:
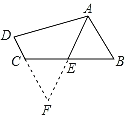
【题目】(1)如图⑴,在△ABC中,∠ABC 、∠ACB的平分线相交于点O,试说明∠BOC=90°+![]() ∠A;
∠A;
(2)如图⑵,在△ABC中,BD、CD分别是∠ABC 、∠ACB的外角平分线,试说明∠D=90°-![]() ∠A;
∠A;
(3)如图⑶,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,试说明∠A=2∠D。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )

A.P为∠A、∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为AC、AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
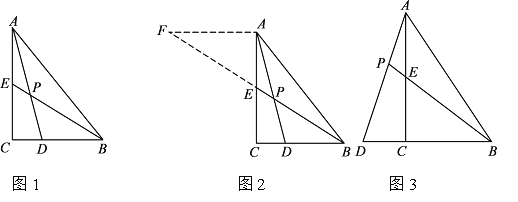
【题目】阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数中,y是x的反比例函数有( )
(1)y=3x;(2)y=﹣![]() ;(3)y=
;(3)y=![]() ;(4)﹣xy=3;(5)
;(4)﹣xy=3;(5)![]() ;(6)
;(6)![]() ;(7)y=2x﹣2;(8)
;(7)y=2x﹣2;(8)![]() .
.
A. (2)(4) B. (2)(3)(5)(8) C. (2)(7)(8) D. (1)(3)(4)(6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.

(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com