
【题目】如图①,BC是⊙O的直径,点A在⊙O上,AD⊥BC垂足为D,弧AE=弧AB,BE分别交AD、AC于点F、G.
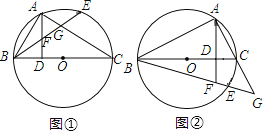
(1)判断△FAG的形状,并说明理由;
(2)如图②若点E与点A在直径BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变(1)中的结论还成立吗?请说明理由.
(3)在(2)的条件下,若BG=26,DF=5,求⊙O的直径BC.
【答案】(1)△FAG是等腰三角形,理由见解析;(2)成立,理由见解析;(3)BC=![]() .
.
【解析】
(1)首先根据圆周角定理及垂直的定义得到∠BAD+∠CAD=90°,∠C+∠CAD=90°,从而得到∠BAD=∠C,然后利用等弧对等角等知识得到AF=BF,从而证得FA=FG,判定等腰三角形;
(2)成立,同(1)的证明方法即可得答案;
(3)由(2)知∠DAC=∠AGB,推出∠BAD=∠ABG,得到F为BG的中点根据直角三角形的性质得到AF=BF=![]() BG=13,求得AD=AF﹣DF=13﹣5=8,根据勾股定理得到BD=12,AB=4
BG=13,求得AD=AF﹣DF=13﹣5=8,根据勾股定理得到BD=12,AB=4![]() ,由∠ABC=∠ABD,∠BAC=∠ADB=90°可证明△ABC∽△DBA,根据相似三角形的性质即可得到结论.
,由∠ABC=∠ABD,∠BAC=∠ADB=90°可证明△ABC∽△DBA,根据相似三角形的性质即可得到结论.
(1)△FAG等腰三角形;理由如下:
∵BC为直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵![]() ,
,
∴∠ABE=∠ACD,
∴∠DAC=∠AGB,
∴FA=FG,
∴△FAG是等腰三角形.
(2)成立,理由如下:
∵BC为直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵![]() ,
,
∴∠ABE=∠ACD,
∴∠DAC=∠AGB,
∴FA=FG,
∴△FAG是等腰三角形.
(3)由(2)知∠DAC=∠AGB,且∠BAD+∠DAC=90°,∠ABG+∠AGB=90°,
∴∠BAD=∠ABG,
∴AF=BF,
∵AF=FG,
∴BF=GF,即F为BG的中点,
∵△BAG为直角三角形,
∴AF=BF=![]() BG=13,
BG=13,
∵DF=5,
∴AD=AF﹣DF=13﹣5=8,
∴在Rt△BDF中,BD=![]() =12,
=12,
∴在Rt△BDA中,AB=![]() =4
=4![]() ,
,
∵∠ABC=∠ABD,∠BAC=∠ADB=90°,
∴△ABC∽△DBA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BC=![]() ,
,
∴⊙O的直径BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .结论:①
.结论:①![]() ;②
;②![]() ≌
≌![]() ;③
;③![]() ∽
∽![]() ;④
;④![]() ;⑤
;⑤![]() .其中的正确的个数是( )
.其中的正确的个数是( )
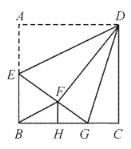
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
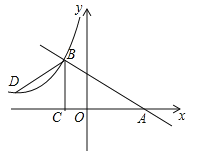
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂接的600件玩具的订单后,决定由甲、乙两车间共同完成生产任务,已知甲车间工作效率是乙车间的2倍,乙车间单独完成此项生产任务比甲车间单独完成多用10天.
(1)求甲,乙两车间平均每天各能制作多少件玩具;
(2)两车间同时开工3天后,临时又增加了90件的玩具生产任务,为了使完成任务的总时间不超过7天,两车间从第4天起各自提高工作效率,提高工作效率后甲车间工作效率仍是乙车间工作率的2倍,求乙车间提高效率后每天至少生产多少件玩具.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片分别写有数字﹣1、﹣3、4、6,将这些卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字大于0的概率是______;
(2)从中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的a,再从余下的卡片中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的b,利用树状图或表格的方法,求出这个二次函数图象的对称轴在y轴右侧的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于⊙
内接于⊙![]() ,
,![]() 是直径,
是直径,![]() ,点
,点![]() 在⊙
在⊙![]() 上.
上.
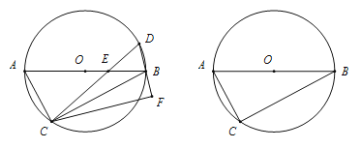
(1)如图,若弦![]() 交直径
交直径![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 是点
是点![]() 到
到![]() 的垂线.
的垂线.
①问![]() 的度数和点
的度数和点![]() 的位置有关吗?请说明理由.
的位置有关吗?请说明理由.
②若![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的正弦值.
的正弦值.
(2)若⊙![]() 的半径长为
的半径长为![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直
,对称轴为直![]() .下列结论:
.下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若点
若点![]() 点
点![]() 点
点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com