
【题目】已知,在四边形![]() 中,
中,![]() 为四边形
为四边形![]() 的
的![]() 的平分线及外角
的平分线及外角![]() 的平分线所在的直线构成的锐角,若
的平分线所在的直线构成的锐角,若![]() ,
,![]() ,
,
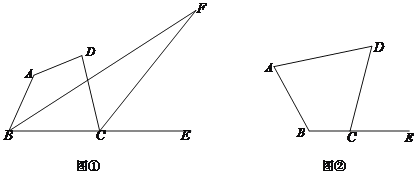
(1)如图①,当![]() >180°时,
>180°时,![]() =_________(用含
=_________(用含![]() ,
,![]() 的式子表示);
的式子表示);
(2)如图②,当![]() <180°时,请在图②中,画出
<180°时,请在图②中,画出![]() ,且
,且![]() ______(用含
______(用含![]() ,
,![]() 的式子表示);
的式子表示);
(3)当![]() ,
,![]() 满足条件_______时,不存在
满足条件_______时,不存在![]() .
.
【答案】(1)![]() 90°;(2)画图见解析;90°-
90°;(2)画图见解析;90°-![]() ;(3)
;(3)![]() 180°.
180°.
【解析】
(1)与(2)先根据四边形内角和等于360°,得出∠ABC+∠DCB=360°-(α+β),再根据邻补角的定义与三角形外角的性质定理和角平分线的定义整理即可得出结论;
(3)当∠F=0°时不存在,代入(1)或(2)题得出的结论即可得出α,β满足的关系式.
解:(1)∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠ECF)
=180°-2(∠ECF-∠FBC)=180°-2∠F,
∴360°-(α+β)=180°-2∠F,
∴![]() ;
;
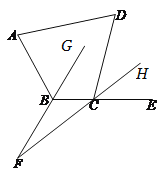
(2)画出的∠F如图所示,∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠GBC+(180°-2∠HCE)
=180°+2(∠GBC-∠HCE)=180°+2(∠GBC-∠BCF)=180°+2∠F,
∴360°-(α+β)=180°+2∠F,
∴![]() ;
;
(3)由以上两题的结论知:当α+β=180°时,∠F=0°,故不存在∠F.
所以当α+β=180°时,不存在∠F.


科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在等腰直角三角形![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .则
.则![]() 、
、![]() 和
和![]() 之间的数量关系是: .
之间的数量关系是: .
(2)如图(2),将(1)中的条件改为:在等腰三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否成立?如成立,请你给出证明;若不成立,请说明理由.
是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点(
上的两动点(![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用手指玩游戏,规则如下:i)每次游戏时,两人同时随机地各伸出一根手指;ii)两人伸出的手指中,大拇指只胜食指,食指只胜中指,中指只胜无名指,无名指只胜小拇指,小拇指只胜大拇指,否则不分胜负,依据上述规则,当甲、乙两人同时随机地各伸出一根手指时,
(1)求甲伸出小拇指取胜的概率;
(2)求乙取胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了一张嘉峪关的门票,她和哥哥都想去,可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽取一张,然后将抽出的两张牌数字相加,如果和为偶数,则小敏去,如果和为奇数,则哥哥去.
(1)请你用列表或树状图的方法求小敏去的概率.
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为点
,垂足为点![]() ,交直线
,交直线![]() 于点
于点![]() .
.![]() 垂直平分
垂直平分![]() ,垂足为点
,垂足为点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图①,若![]() 100°,求
100°,求![]() 的大小;
的大小;
(2)如图②,若![]() 70°,求
70°,求![]() 的大小;
的大小;
(3)若![]() (
(![]() 90°),用含
90°),用含![]() 的式子表示
的式子表示![]() 的大小(直接写出结果即可).
的大小(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
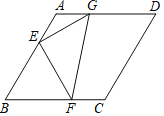
【题目】如图,点E、F、G分别在菱形ABCD的边AB,BC,AD上,AE=![]() AB,CF=
AB,CF=![]() CB,AG=
CB,AG=![]() AD.已知△EFG的面积等于6,则菱形ABCD的面积等于_____.
AD.已知△EFG的面积等于6,则菱形ABCD的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com