
【题目】如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=75°.求∠BED的度数.

【答案】130°
【解析】
由DE∥BC,根据平行线的性质可得出“∠C=∠ADE,∠AED=∠ABC,∠EDB=∠CBD”,根据角平行线的性质可设∠CBD=α,则∠AED=2α,通过角的计算得出α=25°,再依据互补角的性质可得出结论.
∵DE∥BC,
∴∠C=∠ADE,∠AED=∠ABC,∠EDB=∠CBD,
又∵BD平分∠ABC,
∴∠CBD=∠ABD=∠EDB,
设∠CBD=α,则∠AED=2α.
∵∠A+∠AED+∠ADE=180°,∠ADE+∠EDB+∠BDC=180°,
∴∠A+∠AED=∠EDB+∠BDC,即50°+2α=α+75°,
解得:α=25°.
又∵∠BED+∠AED=180°,
∴∠BED=180°-∠AED=180°-25°×2=130°.


科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
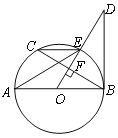
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,如杨辉三角就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数降幂排列)的系数规律例如,在三角形中第一行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3ab+3ab2+b3展开式中的系数.结合对杨辉三角的理解完成以下问题
(1)(a+b)2展开式a2+2ab+b2中每一项的次数都是 次;
(a+b)3展开式a3+3a2b+3ab2+b3中每一项的次数都是 次;
那么(a+b)n展开式中每一项的次数都是 次.
(2)写出(a+1)4的展开式 .
(3)拓展应用:计算(x+1)5+(x﹣1)6+(x+1)7的结果中,x5项的系数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线,若在边BC上截取CE=CB,连接DE,则图中等腰三角形有( )

A.3个B.4个C.5个D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换,例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.現有10×10的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
的另一个格点的运动称为一次跳马变换,例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.現有10×10的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知分式: ![]()
(1)化简这个分式
(2)把分式A化简结果的分子与分母同时加上3后得到分式B,问:当a>2时,分式B的值较原来分式A的值是变大了还是变小了?试说明理由。
(3)若A的值是整数,且a也为整数,求出所有符合条件a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,则:
,则:
①线段PB= ,PC= ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com