
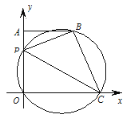
【题目】如图,在平面直角坐标系中,A(0,4),B(3,4),P 为线段 OA 上一动点,过 O,P,B 三点的圆交 x 轴正半轴于点 C,连结 AB, PC,BC,设 OP=m.
(1)求证:当 P 与 A 重合时,四边形 POCB 是矩形.
(2)连结 PB,求 tan∠BPC 的值.
(3)记该圆的圆心为 M,连结 OM,BM,当四边形 POMB 中有一组对边平行时,求所有满足条件的 m 的值.
(4)作点 O 关于 PC 的对称点O ,在点 P 的整个运动过程中,当点O 落在△APB 的内部 (含边界)时,请写出 m 的取值范围.
【答案】(1)见解析;(2)tan∠BPC=![]() ;(3)m=
;(3)m=![]() 或 m=
或 m=![]() ;(4)0≤m≤
;(4)0≤m≤![]() 或 m=
或 m=![]() .
.
【解析】
(1)由∠COA=90°可知PC为直径,所以∠PBC=90°,P、A重合时得3个直角,即证四边形POCB为矩形.
(2)题干已知的边长只有OA、AB,所以要把∠BPC转化到与OA、OB有关的三角形内.连接O,B,根据圆周角定理,得∠COB=∠BPC,又AB∥OC有∠ABP=∠COB,得∠BPC=∠ABO.
(3)分两种情况:①OP∥BM即BM⊥x轴,延长BM交x轴于N,根据垂径定理得ON=CN=3,设半径为r,利用Rt△CMN的三边关系列方程即可求出;②OM∥PB,根据圆周角定理和等腰三角形性质得到△BOM≌△COM,所以BO=CO=5,用m表示各条线段,再利用勾股定理列方程求得m的值.
(4)因为点O与点O'关于直线对称,所以∠PO'C=∠POC=90°,即点O'在圆上;考虑点P运动到特殊位置:①点O'与点O重合;②点O'落在AB上;③点O'与点B重合.算出对应的m值再考虑范围.
(1)∵∠COA=90°,∴PC是直径,∴∠PBC=90°.
∵A(0,4)B(3,4),∴AB⊥y轴,∴当A与P重合时,∠OPB=90°,∴四边形POCB是矩形;
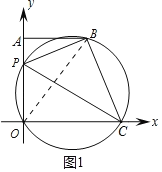
(2)连结OB,(如图1)
∴∠BPC=∠BOC.
∵AB∥OC,∴∠ABO=∠BOC,∴∠BPC=∠BOC=∠ABO,∴tan∠BPC=tan∠ABO![]() ;
;
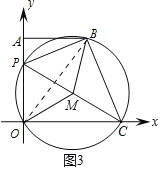
(3)∵PC为直径,∴M为PC中点.
①如图2,当OP∥BM时,延长BM交x轴于点N.
∵OP∥BM,∴BN⊥OC于N,∴ON=NC,四边形OABN是矩形,∴NC=ON=AB=3,BN=OA=4.
设⊙M半径为r,则BM=CM=PM=r,∴MN=BN﹣BM=4﹣r.
∵MN2+NC2=CM2,∴(4﹣r)2+32=r2
解得:r![]() ,∴MN=4
,∴MN=4![]() .
.
∵M、N分别为PC、OC中点,∴m=OP=2MN![]() ;
;

②如图3,当OM∥PB时,∠BOM=∠PBO.
∵∠PBO=∠PCO,∠PCO=∠MOC,∴∠OBM=∠BOM=∠MOC=∠MCO.
在△BOM与△COM中,∵∠BOM=∠COM,∠OBM=∠OCM,BM=CM,∴△BOM≌△COM(AAS),∴OC=OB![]() 5.
5.
∵AP=4﹣m,∴BP2=AP2+AB2=(4﹣m)2+32.
∵∠ABO=∠BOC=∠BPC,∠BAO=∠PBC=90°,∴△ABO∽△BPC,∴![]() ,∴PC
,∴PC![]() ,∴PC2
,∴PC2![]() BP2
BP2![]() [(4﹣m)2+32].
[(4﹣m)2+32].
又PC2=OP2+OC2=m2+52,∴![]() [(4﹣m)2+32]=m2+52
[(4﹣m)2+32]=m2+52
解得:m![]() 或m=10(舍去).
或m=10(舍去).
综上所述:m![]() 或m
或m![]() .
.
(4)∵点O与点O'关于直线对称,∴∠PO'C=∠POC=90°,即点O'在圆上.
当O'与O重合时,得:m=0;
当O'落在AB上时,得:m![]() ;
;
当O'与点B重合时,得:m![]() ;
;
∴0≤m![]() 或m
或m![]() .
.


科目:初中数学 来源: 题型:
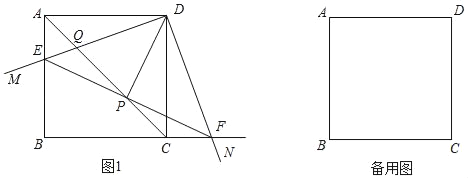
【题目】如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
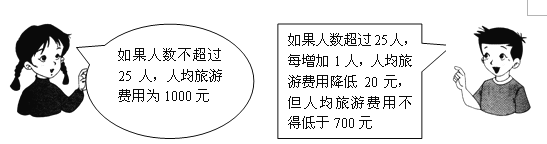 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次模拟考试后,抽取 m 名学生的数学成绩进行整理分组,形成如下表格(x 代表成绩),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A 组 | 140<x≤150 |
B 组 | 130<x≤140 |
C 组 | 120<x≤130 |
D 组 | 110<x≤120 |
E 组 | 100<x≤110 |
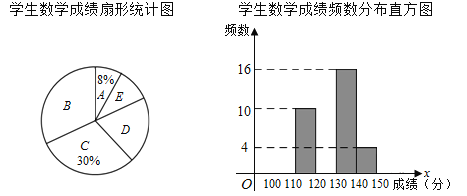
(1)m 的值为多少,扇形统计图中 D 组对应的圆心角是多少度.
(2)请补全条形统计图,并标注出相应的人数.
(3)若此次考试数学成绩 130 分以上的为优秀,参加此次模拟考的学生总数为 2000,请估算此次考试数学成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
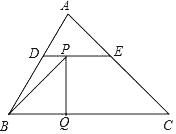
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 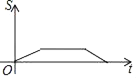 B.
B. 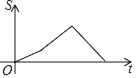
C. 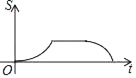 D.
D. 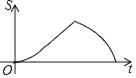
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别写一个满足下列条件的一元二次方程:
方程的两个根相等___________________________________
方程的两根互为相反数______________________________________
方程的两根互为倒数__________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
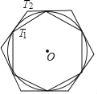
【题目】T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=![]() ;③a:b=1:
;③a:b=1:![]() ;④S1:S2=3:4.其中正确的有_____.(填序号)
;④S1:S2=3:4.其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的条件下,设⊙O的半径为3,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com