
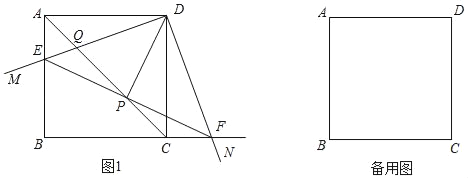
【题目】如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.
(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;
(2)当AE=1时,求PQ的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)①只要证明△ADE≌△CDE(ASA)即可解决问题;
②利用相似三角形的性质证明∠PDQ=45°即可解决问题;
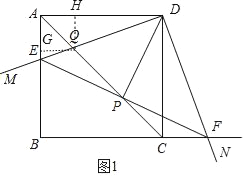
(2)作QH⊥AD于H,QE⊥AB于G.由△AQD∽△EQP,可知AQPQ=DQEQ,想办法求出AQ,EQ,DQ即可解决问题;
(1)①证明:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=∠DAE=∠DCF=90°,
∴∠ADC=∠MDN=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDE(ASA),
∴AE=CF.
②∵△ADE≌△CDE(ASA),
∴DE=DF,∵∠MDN=90°,
∴∠DEF=45°,
∵∠DAC=45°,
∴∠DAQ=∠PEQ,∵∠AQD=∠EQP,
∴△AQD∽△EQP,
∴![]() ,
,
∴![]() ,
,
∵∠AQE=∠PQD,
∴△AQE∽△DQP,
∴∠DDP=∠QAE=45°,
∴∠DPE=90°,
∴DP⊥EF,
∵DE=DF,
∴PE=PF,
∴DP垂直平分线段EF.
(2)解:作QH⊥AD于H,QE⊥AB于G.
在Rt△ADE中,DE=![]() ,
,
∵∠QAH=∠QAG=45°,
∴HO=QE=AH=EQ,设QH=x,
∵![]() ×4×x+
×4×x+![]() ×1×x=
×1×x=![]() ×1×4,
×1×4,
∵x=![]() ,
,
∴AQ=![]() ,DQ=
,DQ=![]() =
=![]() ,EQ=
,EQ=![]() ,
,
∵△AQD∽△EQP,
∴AQPQ=DQEQ,
∴PQ=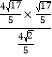 =
=![]() .
.


科目:初中数学 来源: 题型:
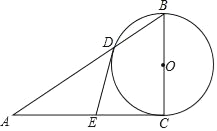
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=8,DE=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
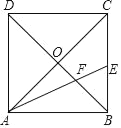
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).

A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
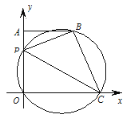
【题目】如图,在平面直角坐标系中,A(0,4),B(3,4),P 为线段 OA 上一动点,过 O,P,B 三点的圆交 x 轴正半轴于点 C,连结 AB, PC,BC,设 OP=m.
(1)求证:当 P 与 A 重合时,四边形 POCB 是矩形.
(2)连结 PB,求 tan∠BPC 的值.
(3)记该圆的圆心为 M,连结 OM,BM,当四边形 POMB 中有一组对边平行时,求所有满足条件的 m 的值.
(4)作点 O 关于 PC 的对称点O ,在点 P 的整个运动过程中,当点O 落在△APB 的内部 (含边界)时,请写出 m 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com