Question

4．如图，在直角坐标系中，直线y=-x+4交矩形OACB于F与G，交x轴于D，交y轴于E．若∠FOG=45°，求矩形OACB的面积8．

Answer 1

分析 根据一次函数解析式求得OD=OE=4，则△EOD是等腰直角三角形，得出∠ODE=∠OED=45°，由∠OGE=∠ODF+∠DOG=45°+∠DOG，∠DOF=∠EOF++∠DOG=45°+∠DOG得出∠DOF=∠OGE，从而证得△DOF∽△EGO，得出$\frac{DF}{OE}$=$\frac{OD}{EG}$，DF•EG=OE•OD=16，过点F作FM⊥x轴于点M，过点G作GN⊥y轴于点N．则易知DF=$\sqrt{2}$b，GE=$\sqrt{2}$a，得出DF•GE=2ab=16，求得ab=8．

解答 解：∵直线y=-x+4与x轴，y轴分别交于点D，点E，
∴OD=OE=4，
∴∠ODE=∠OED=45°；
∴∠OGE=∠ODF+∠DOG=45°+∠DOG，
∵∠EOF=45°，
∴∠DOF=∠EOF++∠DOG=45°+∠DOG，
∴∠DOF=∠OGE，
∴△DOF∽△EGO，
∴$\frac{DF}{OE}$=$\frac{OD}{EG}$，
∴DF•EG=OE•OD=16，
过点F作FM⊥x轴于点M，过点G作GN⊥y轴于点N．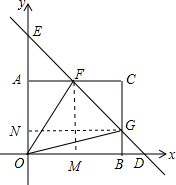
∴△DMF和△ENG是等腰直角三角形，
∵NG=AC=a，FM=BC=b，
∴DF=$\sqrt{2}$b，GE=$\sqrt{2}$a，
∴DF•GE=2ab，
∴2ab=16，
∴ab=8，
∴矩形OACB的面积=ab=8．
故答案为8．

点评 本题是一次函数的综合题，考查了一次函数图象上点的坐标特征，三角形相似的判定和性质找出辅助线构建等腰直角三角形，求得DF=$\sqrt{2}$b，GE=$\sqrt{2}$a是解题的关键．