
如图①,已知抛物线C1: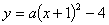 的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及 a 的值;
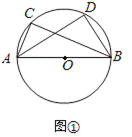
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3.C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
 |  | ||
解:(1)顶点C为(-1,-4) ………………………………………1分
∵点B(1,0)在抛物线C1上,∴ ,解得,a=1 ………2分
,解得,a=1 ………2分
(2)①∵C2与C1关于x轴对称,∴抛物线C2的表达式为 ……3分
……3分
抛物线C3由C2平移得到,∴抛物线C3为 ……4分
……4分
∴E(5,0)
设直线CE的解析式为:y=kx+b,
则 ,解得
,解得 ,…………………………………………………5分
,…………………………………………………5分
∴直线BC的解析式为y= x﹣
x﹣ , …………………………………………………6分
, …………………………………………………6分
设P(x,﹣x2+6x﹣5),则F(x, x﹣
x﹣ ),
),
∴PF=(﹣x2+6x﹣5)﹣( x﹣
x﹣ )=﹣x2+
)=﹣x2+ x﹣
x﹣ =﹣(x﹣
=﹣(x﹣ )2+
)2+ ,………8分
,………8分
∴当x= 时,PF有最大值为
时,PF有最大值为 .…………………………………………………9分
.…………………………………………………9分
②若PE=EF,∵ PF⊥x轴,∴x轴平分PF,
∴﹣x2+6x﹣5=- x+
x+ , …………………………………………………10分
, …………………………………………………10分
解得x1= ,x2=5(舍去)
,x2=5(舍去)
∴P( ,
, ).
).


科目:初中数学 来源: 题型:
已知关于x的一元二次方程x2-x+m =0有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2,且2x1·x2=m2-3,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
以下命题:①直径相 等的圆是等圆; ②长度相等弧是等弧; ③一个圆只有一条直径 ;④直径是圆中最长的弦.其中正确的个数是……………………………………
等的圆是等圆; ②长度相等弧是等弧; ③一个圆只有一条直径 ;④直径是圆中最长的弦.其中正确的个数是…………………………………… ……( )
……( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
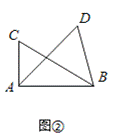

小明尝试用反证法:如图③,过A、B、C三点作圆,圆心为O,假设点D在圆O外,设AD交圆O于点E,连接BE,则∠AEB=∠ACB,又由∠AEB是△BDE的一个外角,得∠AEB>∠ADB,因此∠ACB>∠ADB,就与条件∠ACB=∠ADB相矛盾,所以点D不在圆O外。
点D可能在⊙O内吗?,请你补全小明的解题过程(画出示意图)并给出你的结论。
【应用】
利用【发现】和【思考】中的结论解决问题:
(1)如图④,四边形ABCD是正方形,点E为BC上的任一点,AE⊥EF,EF交∠BCD的外 角平分线于点F.求证:EA=EF.
角平分线于点F.求证:EA=EF.
(2)如图⑤,正方形ABCD的中心为O,面积为1989cm2.P为正方形内一点,且∠OPB=45°,PA:PB=5:14.求OP长度
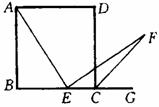
图④ 图⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有( )
①AP=BP; ②BP= AB; ③AB=2AP; ④AP+PB=AB。
AB; ③AB=2AP; ④AP+PB=AB。
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com