
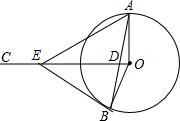
 如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE
如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE分析 (1)由OC⊥OA,得到∠AOD=90°,根据OA=OB,求得∠DAO=∠DBO,根据线段垂直平分线的性质得到ED=EB,求得∠EDB=∠EBD,等量代换得到∠ECO=90°,于是证得结论;
(2)由∠OAB=22.5°,求出∠OBD=22.5°,于是得到∠EBD=∠EDB=67.5°,推出∠DEB=45°,得到△BEO是等腰直角三角形,于是得到OE=$\sqrt{2}$,即可得到结果.
解答 解: (1)∵OC⊥OA,
(1)∵OC⊥OA,
∴∠AOD=90°,
∵OA=OB,
∴∠DAO=∠DBO,
∵点E是BD的垂直平分线与OC的交点,
∴ED=EB,
∴∠EDB=∠EBD,
∵∠ADO=∠EDB,
∴∠ECD+∠DBO=∠ADO+∠DAO=90°,
∴∠ECO=90°,
∴BE是⊙O的切线;
(2)∵∠OAB=22.5°,
∴∠OBD=22.5°,
∴∠EBD=∠EDB=67.5°,
∴∠DEB=45°,
∴BE=OB=OA=1,
∴OE=$\sqrt{2}$,
∴S四边形AOBE=S△OBE+S△AOE=$\frac{1}{2}×1×1$$+\frac{1}{2}×1×\sqrt{2}$=$\frac{1}{2}$$+\frac{\sqrt{2}}{2}$.
点评 本题考查了切线的判定,线段垂直平分线的性质,解直角三角形,三角形的面积,正确的识别图形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
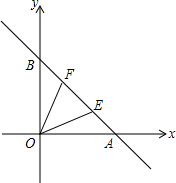 如图,直线y=-x+1与两坐标轴分别交于A、B两点,E、F为线段AB上的两个动
如图,直线y=-x+1与两坐标轴分别交于A、B两点,E、F为线段AB上的两个动查看答案和解析>>
科目:初中数学 来源: 题型:解答题
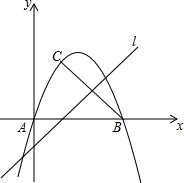 我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知动点(x,y)的横纵坐标满足方程2y-x=2.
已知动点(x,y)的横纵坐标满足方程2y-x=2.| 点的名称 | A | B | C | D | E |
| 点的横坐标x | -2 | 2 | |||
| 点的纵坐标y | -1 | 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
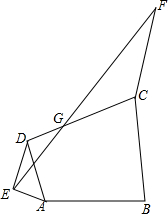 如图,在四边形ABCD中,∠ABC=90°,DE⊥AE于点E,CF∥ED,连接EF交CD边于点G,试判断∠EAB与∠FCB有怎样的数量关系,写出你的猜想,并加以证明.
如图,在四边形ABCD中,∠ABC=90°,DE⊥AE于点E,CF∥ED,连接EF交CD边于点G,试判断∠EAB与∠FCB有怎样的数量关系,写出你的猜想,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com