
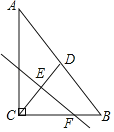
【题目】如图所示,在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,作CD的中垂线与CD交于点E,与BC交于点F.若CF=x,tanA=y,则x与y之间满足( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由直角三角形斜边上的中线性质得出CD=![]() AB=AD=4,由等腰三角形的性质得出∠A=∠ACD,得出tan∠ACD=
AB=AD=4,由等腰三角形的性质得出∠A=∠ACD,得出tan∠ACD=![]() =tanA=y,证明△CEG∽△FEC,得出
=tanA=y,证明△CEG∽△FEC,得出![]() ,得出y=
,得出y=![]() ,求出y2=
,求出y2=![]() ,得出
,得出![]() =FE2,再由勾股定理得出FE2=CF2﹣CE2=x2﹣4,即可得出答案.
=FE2,再由勾股定理得出FE2=CF2﹣CE2=x2﹣4,即可得出答案.
解:如图所示:
∵在△ABC中,∠C=90°,AB=8,CD是AB边上的中线,
∴CD=![]() AB=AD=4,
AB=AD=4,
∴∠A=∠ACD,
∵EF垂直平分CD,
∴CE=![]() CD=2,∠CEF=∠CEG=90°,
CD=2,∠CEF=∠CEG=90°,
∴tan∠ACD=![]() =tanA=y,
=tanA=y,
∵∠ACD+∠FCE=∠CFE+∠FCE=90°,
∴∠ACD=∠FCE,
∴△CEG∽△FEC,
∴![]() =
=![]() ,
,
∴y=![]() ,
,
∴y2=![]() ,
,
∴![]() =FE2,
=FE2,
∵FE2=CF2﹣CE2=x2﹣4,
∴![]() =x2﹣4,
=x2﹣4,
∴![]() +4=x2,
+4=x2,
故选:A.


科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
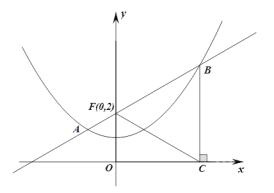
【题目】如图1,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的右侧),与
的右侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 、
、![]() 、
、![]() 的坐标:
的坐标:
(2)当以![]() 为圆心的圆与
为圆心的圆与![]() 轴和直线
轴和直线![]() 都相切时,求抛物线的解析式:
都相切时,求抛物线的解析式:
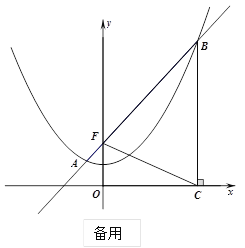
(3)在(2)的条件下,如图2.![]() 是
是![]() 轴负半轴上的一点,过点
轴负半轴上的一点,过点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ,使得
,使得![]() 恰好落在
恰好落在![]() 轴上?若存在,请求出
轴上?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的交点
轴的交点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
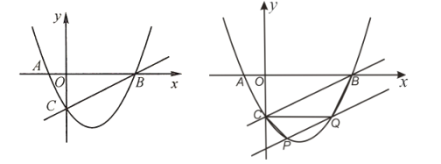
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,过点
下方抛物线上的一点,过点![]() 作
作![]() 的平行线交抛物线于点
的平行线交抛物线于点![]() (点
(点![]() 在点
在点![]() 右侧),连结
右侧),连结![]() 、
、![]() ,当
,当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 点的坐标;
点的坐标;
(3)现将该抛物线沿射线![]() 的方向进行平移,平移后的抛物线与直线
的方向进行平移,平移后的抛物线与直线![]() 的交点为
的交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的下方),与
的下方),与![]() 轴的右侧交点为
轴的右侧交点为![]() ,当
,当![]() 与
与![]() 相似,求出点
相似,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中数学 来源: 题型:
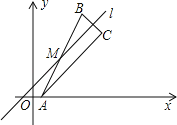
【题目】对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(1,0).如图,点M是直线l上的一点,点A关于点M的对称点为点B,点B关于直线l的对称点为点C.若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),则点B的坐标为_____及n的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某段地铁工程由甲、乙两工程队合作![]() 天可完成.若单独施工,甲工程队比乙工程队多用
天可完成.若单独施工,甲工程队比乙工程队多用![]() 天.
天.
![]() 求甲、乙两工程队单独完成此项工程各需要多少天?
求甲、乙两工程队单独完成此项工程各需要多少天?
![]() 如果甲工程队施工每天需付施工费
如果甲工程队施工每天需付施工费![]() 万元,乙工程队施工每天需付施工费
万元,乙工程队施工每天需付施工费![]() 万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过
万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过![]() 万元?
万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com