
【题目】如图,在以点![]() 为中心的正方形
为中心的正方形![]() 中,
中,![]() ,连接
,连接![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 以每秒1个单位长度的速度匀速运动,到达点
以每秒1个单位长度的速度匀速运动,到达点![]() 停止.在运动过程中,
停止.在运动过程中,![]() 的外接圆交
的外接圆交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() .
.
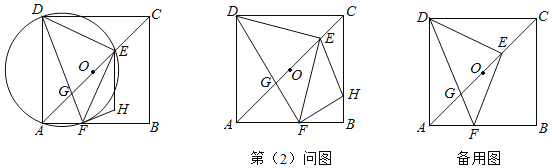
(1)求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(2)当点![]() 恰好落在线段
恰好落在线段![]() 上时,求
上时,求![]() 的长;
的长;
(3)设点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于时间
关于时间![]() 的关系式.
的关系式.
【答案】(1)证明见解析;(2)EH![]() ;(3)
;(3)![]() .
.
【解析】
(1)由正方形的性质可得![]() ,再根据圆周角定理即可证得结论;
,再根据圆周角定理即可证得结论;
(2)设![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 可得
可得![]() ,再证明
,再证明![]() 可得
可得![]() 与t的关系式,进一步可表示
与t的关系式,进一步可表示![]() 的长,由
的长,由![]() 得比例线段
得比例线段![]() ,进而求出
,进而求出![]() 的值,然后代入
的值,然后代入![]() 的表达式可求
的表达式可求![]() 的值;
的值;
(3)由(2)知![]() 与t的关系式,再过点
与t的关系式,再过点![]() 作
作![]() 于点
于点![]() ,易证
,易证![]() ,于是
,于是![]() ,再根据三角形的面积公式即可求解.
,再根据三角形的面积公式即可求解.
(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;

(2)设![]() ,连接
,连接![]() ,如图,则
,如图,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当点![]() 恰好落在线段
恰好落在线段![]() 上时,
上时,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵FG=FH,∴![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴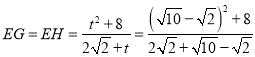
![]() ;
;

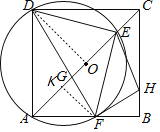
(3)过点![]() 作
作![]() 于点
于点![]() ,由(2)得
,由(2)得![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆,售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元,每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加![]() 盆,第二期盆景与花卉售完后的利润分别为
盆,第二期盆景与花卉售完后的利润分别为![]() ,
,![]() (单位:元)
(单位:元)
(1)用含![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() .
.
(2)当![]() 取何值时,第二期培植的盆录与花卉售完后获得的总利润
取何值时,第二期培植的盆录与花卉售完后获得的总利润![]() 最大,最大总利润是多少?
最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .点
.点![]() 为
为![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 切
切![]() 于点
于点![]() ,设
,设![]() .
.
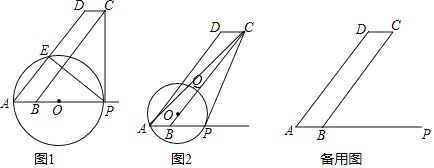
(1)如图1,![]() 为何值时,圆心
为何值时,圆心![]() 落在
落在![]() 上?若此时
上?若此时![]() 交
交![]() 于点
于点![]() ,直接指出PE与BC的位置关系;
,直接指出PE与BC的位置关系;
(2)当![]() 时,如图2,
时,如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数,并通过计算比较弦
的度数,并通过计算比较弦![]() 与劣弧
与劣弧![]() 长度的大小;
长度的大小;
(3)当![]() 与线段
与线段![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ax2 + bx +c经过点A(-1,0), B(3,0), C(0,-3).
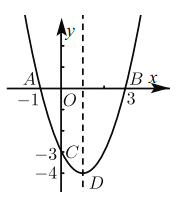
(1)求该二次函数的解析式.
(2)利用图象的特点填空.
①当x= ___ 时方程ax2 + bx+c=-3.
当x= ___时方程ax2 +bx+c=-4.
②不等式ax2 + bx + c> 0的解集为
不等式-4<ax2+bx+c<0的解集为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学为丰富同学们的校园生活,举行“校园电视台主待人”选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
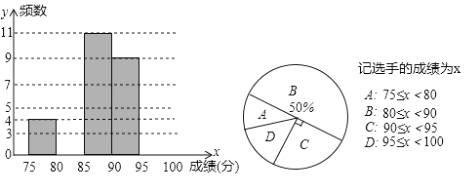
请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形![]() 对应的圆心角度数;
对应的圆心角度数;
(2)成绩在![]() 区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为对角线BD上的一点,点F在AD的延长线上,且∠CEF=90°,EF交CD于H,分别过点F,点C作EC和EF的平行线,交于点G.
(1)证明:AE=CE;
(2)证明:四边形ECGF是正方形;
(3)若正方形ABCD的边长为![]() ,且BE=BC,求此时ΔEDF的面积.
,且BE=BC,求此时ΔEDF的面积.
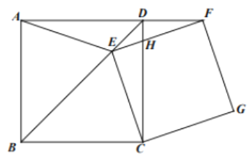
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在上午的某一时刻,阳光下身高1.7米的小刚在地面上的影长为3.4米,小明测得同一校园中旗杆在地面上的影子长16米,还有2米影子落在与地面垂直的墙上,根据这些条件可以知道旗杆的高度为_______m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com