
【题目】如图1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .点
.点![]() 为
为![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 切
切![]() 于点
于点![]() ,设
,设![]() .
.
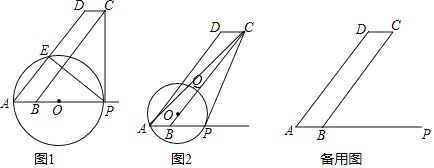
(1)如图1,![]() 为何值时,圆心
为何值时,圆心![]() 落在
落在![]() 上?若此时
上?若此时![]() 交
交![]() 于点
于点![]() ,直接指出PE与BC的位置关系;
,直接指出PE与BC的位置关系;
(2)当![]() 时,如图2,
时,如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数,并通过计算比较弦
的度数,并通过计算比较弦![]() 与劣弧
与劣弧![]() 长度的大小;
长度的大小;
(3)当![]() 与线段
与线段![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)当x=9时,圆心O落在AP上,PE⊥BC;(2)∠CAP=45°,弦AP的长度>劣弧![]() 长度;(3)x≥18.
长度;(3)x≥18.
【解析】
(1)由三角函数定义知:Rt△PBC中,![]() tan∠PBC=tan∠DAB
tan∠PBC=tan∠DAB![]() ,设CP=4k,BP=3k,由勾股定理可求得BC,根据“直径所对的圆周角是直角”可得PE⊥AD,由此可得PE⊥BC;
,设CP=4k,BP=3k,由勾股定理可求得BC,根据“直径所对的圆周角是直角”可得PE⊥AD,由此可得PE⊥BC;
(2)作CG⊥AB,运用勾股定理和三角函数可求CG和AG,再应用三角函数求∠CAP,应用弧长公式求劣弧![]() 长度,再比较它与AP长度的大小;
长度,再比较它与AP长度的大小;
(3)当⊙O与线段AD只有一个公共点时,⊙O与AD相切于点A,或⊙O与线段DA的延长线相交于另一点,此时,BP有最小值,即x≥18.
(1)如图1,AP经过圆心O.
∵CP与⊙O相切于P,∴∠APC=90°.
∵ABCD,∴AD∥BC,∴∠PBC=∠DAB,∴![]() tan∠PBC=tan∠DAB
tan∠PBC=tan∠DAB![]() ,设CP=4k,BP=3k,由CP2+BP2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BP=3×3=9,故当x=9时,圆心O落在AP上;
,设CP=4k,BP=3k,由CP2+BP2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BP=3×3=9,故当x=9时,圆心O落在AP上;
∵AP是⊙O的直径,∴∠AEP=90°,∴PE⊥AD.
∵ABCD,∴BC∥AD,∴PE⊥BC.
(2)如图2,过点C作CG⊥AP于G.
∵ABCD,∴BC∥AD,∴∠CBG=∠DAB,∴![]() tan∠CBG=tan∠DAB
tan∠CBG=tan∠DAB![]() ,设CG=4m,BG=3m,由勾股定理得:(4m)2+(3m)2=152,解得:m=3,∴CG=4×3=12,BG=3×3=9,PG=BG﹣BP=9﹣4=5,AP=AB+BP=3+4=7,∴AG=AB+BG=3+9=12,∴tan∠CAP
,设CG=4m,BG=3m,由勾股定理得:(4m)2+(3m)2=152,解得:m=3,∴CG=4×3=12,BG=3×3=9,PG=BG﹣BP=9﹣4=5,AP=AB+BP=3+4=7,∴AG=AB+BG=3+9=12,∴tan∠CAP![]() 1,∴∠CAP=45°;
1,∴∠CAP=45°;
连接OP,OQ,过点O作OH⊥AP于H,则∠POQ=2∠CAP=2×45°=90°,PH![]() AP
AP![]() .
.
在Rt△CPG中,![]() 13.
13.
∵CP是⊙O的切线,∴∠OPC=∠OHP=90°,∠OPH+∠CPG=90°,∠PCG+∠CPG=90°,∴∠OPH=∠PCG,∴△OPH∽△PCG,∴![]() ,即PH×CP=CG×OP,
,即PH×CP=CG×OP,![]() 13=12OP,∴OP
13=12OP,∴OP![]() ,∴劣弧
,∴劣弧![]() 长度
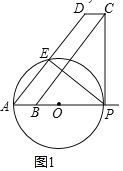
长度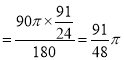 .
.
∵![]() 2π<7,∴弦AP的长度>劣弧
2π<7,∴弦AP的长度>劣弧![]() 长度.
长度.
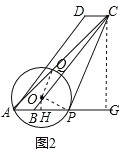
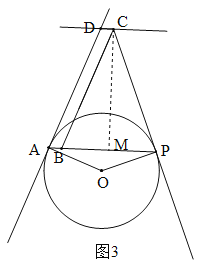
(3)当⊙O与线段AD只有一个公共点时,⊙O与AD相切于点A,或⊙O与线段DA的延长线相交于另一点,此时圆心O位于直线AB下方,且∠OAD≥90°,当∠OAD=90°,∠CPM=∠DAB时,即⊙O与DA切于点A时,BP取得最小值,如图3,过点C作CM⊥AB于M.
∵∠DAB=∠CBP,∴∠CPM=∠CBP,∴CB=CP.
∵ABCD,∴AD∥BC,∴∠PBC=∠DAB,∴tan∠PBC=tan∠DAB![]() ,设CM=4k,BM=3k,由CM2+BM2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BM=3×3=9.
,设CM=4k,BM=3k,由CM2+BM2=BC2,得(4k)2+(3k)2=152,解得:k1=﹣3(舍去),k2=3,∴x=BM=3×3=9.
∵CM⊥AB,∴BP=2BM=2×9=18,∴x≥18.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).

A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
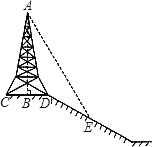
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=20m,DE=30m,小明和小华的身高都是1.5m,同一时刻,小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为2,以点
的边长为2,以点![]() 为圆心,1为半径作圆,
为圆心,1为半径作圆,![]() 是圆
是圆![]() 上的任意一点,将点
上的任意一点,将点![]() 绕点
绕点![]() 按逆时针方向转转
按逆时针方向转转![]() ,得到点
,得到点![]() ,连接
,连接![]() ,则
,则![]() 的最大值是__________.
的最大值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
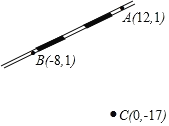
【题目】勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为______km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为______km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,平均每天赢利1200元.
(2)每件童装售价为多少元时,平均每天赢利最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
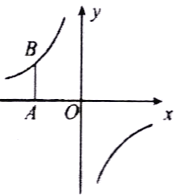
【题目】如图,在平面直角坐标系中,将坐标原点![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位长度得到点
个单位长度得到点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交反比例函数
轴的平行线交反比例函数![]() 的图象于点
的图象于点![]() ,
,![]() .
.
(1)求反比例函数的解析式;
(2)若![]() 、
、![]() 是该反比例函数图象上的两点,且当
是该反比例函数图象上的两点,且当![]() 时,
时,![]() ,指出点
,指出点![]() 、
、![]() 各位于哪个象限?并简要说明理由.
各位于哪个象限?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以点![]() 为中心的正方形
为中心的正方形![]() 中,
中,![]() ,连接
,连接![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 以每秒1个单位长度的速度匀速运动,到达点
以每秒1个单位长度的速度匀速运动,到达点![]() 停止.在运动过程中,
停止.在运动过程中,![]() 的外接圆交
的外接圆交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() .
.
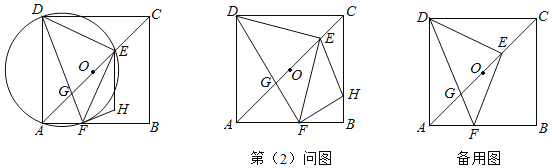
(1)求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(2)当点![]() 恰好落在线段
恰好落在线段![]() 上时,求
上时,求![]() 的长;
的长;
(3)设点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求
,求![]() 关于时间
关于时间![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com