练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

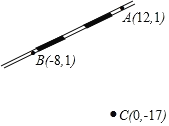
    【题目】勘测队按实际需要构建了平面直角坐标系，并标示了A，B，C三地的坐标，数据如图（单位：km）．笔直铁路经过A，B两地．

    （1）A，B间的距离为______km；

    （2）计划修一条从C到铁路AB的最短公路l，并在l上建一个维修站D，使D到A，C的距离相等，则C，D间的距离为______km．

    【答案】20 13

    【解析】

    （1）由垂线段最短以及根据两点的纵坐标相同即可求出AB的长度；

    （2）根据A、B、C三点的坐标可求出CE与AE的长度，设CD=x，根据勾股定理即可求出x的值．

    （1）由A、B两点的纵坐标相同可知：AB∥x轴，∴AB=12﹣（﹣8）=20；

    （2）过点C作l⊥AB于点E，连接AC，作AC的垂直平分线交直线l于点D，由（1）可知：CE=1﹣（﹣17）=18，AE=12，设CD=x，∴AD=CD=x，由勾股定理可知：x2=（18﹣x）2+122，∴解得：x=13，∴CD=13．

    故答案为：（1）20；（2）13．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解下列一元二次方程

    (1) (2x-1)2=25

    (2) 3x2-6x-1=0

    (3) x2-4x-396=0

    (4) (2-3x)+(3x-2)2=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】是指空气中直径小于或等于的颗粒物，它对人体健康和大气环境造成不良影响，下表是根据《全国城市空气质量报告》中的部分数据制作的统计表．根据统计表回答下列问题，

    （1）2018年7～12月平均浓度的中位数为　 　；

    （2）“扇形统计图”和“折线统计图”中，更能直观地反映2018年7～12月平均浓度变化过程和趋势的统计图是　 　；

    （3）某同学观察统计表后说：“2018年7～12月与2017年同期相比，空气质量有所改善”，请你用一句话说明该同学得出这个结论的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题原型）如图，在中，对角线的垂直平分线交于点，交于点，交于点.求证：四边形是菱形.

    （小海的证法）证明：

    是的垂直平分线，

    ，（第一步）

    ，（第二步）

    .（第三步）

    四边形是平行四边形.（第四步）

    四边形是菱形. （第五步）

    （老师评析）小海利用对角线互相平分证明了四边形是平行四边形，再利用对角线互相垂直证明它是菱形，可惜有一步错了.

    （挑错改错）（1）小海的证明过程在第________步上开始出现了错误.

    （2）请你根据小海的证题思路写出此题的正确解答过程，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某新建火车站站前广场需要绿化的面积为46000米2，施工队在绿化了22000米2后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．

    （1）该项绿化工程原计划每天完成多少米2？

    （2）该项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1和2，中，AB=3，BC=15，．点为延长线上一点，过点作切于点，设．

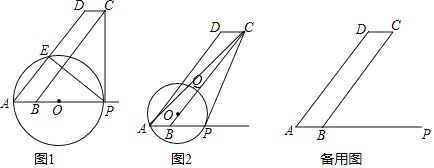
    （1）如图1，为何值时，圆心落在上？若此时交于点，直接指出PE与BC的位置关系；

    （2）当时，如图2，与交于点，求的度数，并通过计算比较弦与劣弧长度的大小；

    （3）当与线段只有一个公共点时，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，中，，，，分别以、、为边作正方形、、，再作，使，点在边上，点、在边上，点、在边上，则的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】胜利中学为丰富同学们的校园生活，举行“校园电视台主待人”选拔赛，现将36名参赛选手的成绩(单位：分)统计并绘制成频数分布直方图和扇形统计图，部分信息如下：

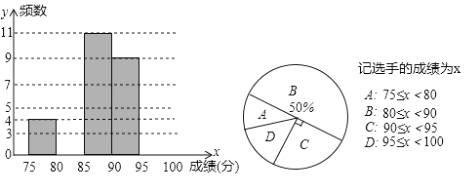
    请根据统计图的信息，解答下列问题：

    (1)补全频数分布直方图，并求扇形统计图中扇形对应的圆心角度数；

    (2)成绩在区域的选手，男生比女生多一人，从中随机抽取两人临时担任该校艺术节的主持人，求恰好选中一名男生和一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正方形OABC的边长为a．直线y＝bx+c交x轴于E，交y轴于F，且a、b、c分别满足﹣（a﹣4）2≥0，c＝+8.

    （1）求直线y＝bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标；

    （2）直线y＝bx+c沿x轴正方向以每秒移动1个单位长度的速度平移，设平移的时间为t秒，问是否存在t的值，使直线EF平分正方形OABC的面积？若存在，请求出t的值；若不存在，请说明理由；

    （3）点P为正方形OABC的对角线AC上的动点（端点A、C除外），PM⊥PO，交直线AB于M，求的值．

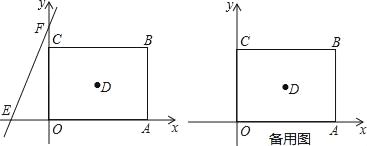
    查看答案和解析>>

    同步练习册答案