
【题目】用适当的方法解下列一元二次方程
(1) (2x-1)2=25
(2) 3x2-6x-1=0
(3) x2-4x-396=0
(4) (2-3x)+(3x-2)2=0
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() ,
,![]() .
.
【解析】
(1)用直接开平方法求解即可;
(2)用公式法求解即可;
(3)用因式分解法求解即可;
(4)用因式分解法求解即可.
(1) ∵(2x-1)2=25,
∴2x-1=±5,
∴2x-1=5或2x-1=-5,
∴![]() ,
,![]() ;
;
(2) ∵ 3x2-6x-1=0,
∴a=3,b=-6,c=-1,
∴=36+12=48,
∴x=![]() ,
,
∴ ![]() ,
,![]() ;
;
(3) ∵ x2-4x-396=0 ,
∴(x-22)(x+18)=0,
∴![]() ,
,![]() ;
;
(4) ∵(2-3x)+(3x-2)2=0,
∴ (3x-2)2-(3x-2)=0,
∴(3x-2) (3x-2-1)=0,
∴3x-2=0或3x-2-1=0,
∴![]() ,
,![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
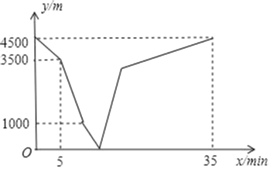
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
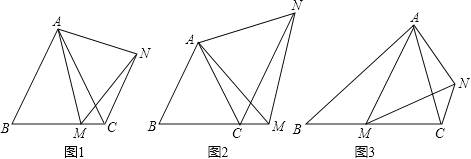
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 交边
交边![]() 于点
于点![]() .
.
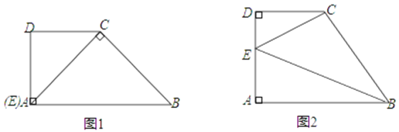
(1)当点![]() 与
与![]() 恰好重合时(如图1),求
恰好重合时(如图1),求![]() 的长;
的长;
(2)问:是否可能使![]() 、
、![]() 与
与![]() 都相似?若能,请求出此时
都相似?若能,请求出此时![]() 的长;若不能,请说明理由(如图2).
的长;若不能,请说明理由(如图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).

A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一段长为![]() 的篱笆围成一个一边靠墙的矩形花圃
的篱笆围成一个一边靠墙的矩形花圃![]() ,墙长
,墙长![]() .设
.设![]() 长为
长为![]() ,矩形的面积为
,矩形的面积为![]() .
.
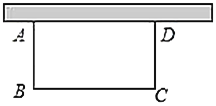
(1)写出![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 长为多少米时,所围成的花圃面积最大?最大值是多少?
长为多少米时,所围成的花圃面积最大?最大值是多少?
(2)当花圃的面积为![]() 时,
时,![]() 长为多少米?
长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
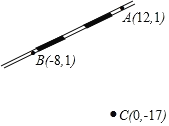
【题目】勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为______km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为______km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com