
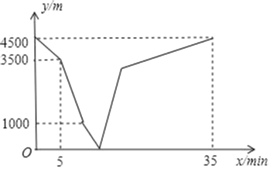
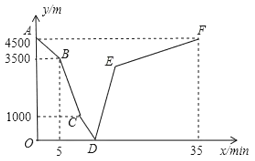
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
【答案】3000
【解析】
分析图象:点A表示出发前两人相距4500米,即举子园和博物馆相距4500米;线段AB表示雪松已跑步出发,两人相距距离逐渐减小,到5分钟时相距3500米,即雪松5分钟走了1000米,可求雪松跑步的速度;线段BC表示余乐乐5分钟后开始出发;点C表示两人相距1000米时,雪松改为步行,可设雪松跑步a分钟,则后面(35a)分钟步行,列方程可求出a,然后用4500减1000再减去雪松走的路程可求出此时余乐乐骑车走的路程,即求出余乐乐的速度;点D表示两人相遇;线段DE表示两人相遇后继续往前走,点E表示余乐乐到举子园,可用路程除以余乐乐的速度得到此时为第几分钟;至此即可求出雪松离举子园的距离.
解:由图象可得:举子园和博物馆相距4500米,
雪松的跑步速度为:(45003500)÷5=200(米/分钟),
∴雪松步行的速度为:200×![]() =100(米/分钟),
=100(米/分钟),
设雪松在第a分钟时改为步行,
列方程得:200a+100(35a)=4500,
解得:a=10,
∴余乐乐骑车速度为:(4500200×101000)÷(105)=300(米/分钟),
∴余乐乐到举子园时的时间为第4500÷300+5=20分钟,
此时雪松离举子园的距离为:200×10+100×10=3000(米),
故答案为:3000.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
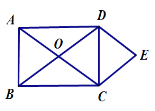
(1)试判断四边形OCED的形状,并说明理由;
(2)若∠DOC = 60°,BC = 6,求矩形ABCD的对角线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泗县某童装专卖店在销售中发现,一款童装每件进价为![]() 元,利润为
元,利润为![]() 元时,每天可售出
元时,每天可售出![]() 件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价
件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价![]() 元,那么平均每天可售出
元,那么平均每天可售出![]() 件.
件.
(1)设每件童装降价![]() 元,每天可售出 件,每件盈利 元,若商家平均每天能赢利
元,每天可售出 件,每件盈利 元,若商家平均每天能赢利![]() 元,每件童装应降价多少元?根据题意,列出方程 .
元,每件童装应降价多少元?根据题意,列出方程 .
(2)利用配方法解答(1)中所列方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为8的正方形ABCD中,点P在BC边上,CP=2,点Q为线段AP上一动点,射线BQ与正方形ABCD的一边交于点R,且AP=BR,那么![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
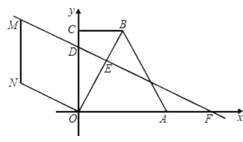
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() 边所在直线为
边所在直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求点![]() 的坐标;
的坐标;
(2)已知![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点E作EG⊥x轴于G,且EG:OG=2.求直线
,过点E作EG⊥x轴于G,且EG:OG=2.求直线![]() 的解析式;
的解析式;
(3)点![]() 是(2)中直线
是(2)中直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上方的平面内是否存在一点
轴上方的平面内是否存在一点![]() ,使以
,使以![]() 为顶点的四边形为菱形?若存在,请求出
为顶点的四边形为菱形?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九月份,开州本地弥猴桃全面上市,其中新品种金梅弥猴桃因其个大多汁而深受大家喜爱,但弥猴桃一直因保鲜技术问题销售量不多,今年终于突破保鲜技术,水果售量明显上升.永辉超市准备大量进货,已知去年同期普通弥猴桃进价3元/斤,金梅弥猴桃进价10元/斤,去年九月共进货900斤.
(1)若去年九月两种弥猴桃进货总价不超过6200元,则金梅弥猴桃最多能购进多少斤?
(2)若永辉超市今年九月上半月共购进1000斤弥猴桃,其中普通弥猴桃进价与去年相同,金梅弥猴桃进价降4元,结果普通弥猴桃按8元/斤,金梅弥猴桃按16元/斤的价格卖出后共获利8000元,下半月因临近祖国七十华诞,水果需量上升,两种弥猴桃进价在上半月基础上保持不变,售价一路上涨,超市调整计划,普通弥猴桃进货量与上半月持平,售价下降a%吸引顾客;金梅弥猴桃进货量上涨生![]() %,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
%,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
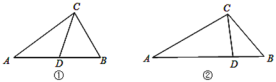
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
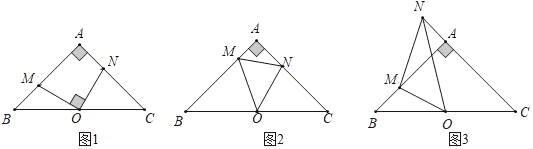
【题目】在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.
(1)如图1,当α=90°时,求证:AM=CN;
(2)如图2,当α=45°时,问线段BM、MN、AN之间有何数量关系,并证明;
(3)如图3,当α=45°时,旋转∠MON,问线段之间BM、MN、AN有何数量关系?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列一元二次方程
(1) (2x-1)2=25
(2) 3x2-6x-1=0
(3) x2-4x-396=0
(4) (2-3x)+(3x-2)2=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com