
【题目】九月份,开州本地弥猴桃全面上市,其中新品种金梅弥猴桃因其个大多汁而深受大家喜爱,但弥猴桃一直因保鲜技术问题销售量不多,今年终于突破保鲜技术,水果售量明显上升.永辉超市准备大量进货,已知去年同期普通弥猴桃进价3元/斤,金梅弥猴桃进价10元/斤,去年九月共进货900斤.
(1)若去年九月两种弥猴桃进货总价不超过6200元,则金梅弥猴桃最多能购进多少斤?
(2)若永辉超市今年九月上半月共购进1000斤弥猴桃,其中普通弥猴桃进价与去年相同,金梅弥猴桃进价降4元,结果普通弥猴桃按8元/斤,金梅弥猴桃按16元/斤的价格卖出后共获利8000元,下半月因临近祖国七十华诞,水果需量上升,两种弥猴桃进价在上半月基础上保持不变,售价一路上涨,超市调整计划,普通弥猴桃进货量与上半月持平,售价下降a%吸引顾客;金梅弥猴桃进货量上涨生![]() %,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
%,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
【答案】(1)500;(2)25
【解析】
(1)设购进金梅弥猴桃x斤,则购进普通弥猴桃(900x)斤,根据单价×数量=总价结合去年九月两种弥猴桃进货总价不超过6200元,即可得出关于x的一元一次不等式,解之取其最大值即可得出结论;
(2)设该超市今年九月上半月购进普通弥猴桃y斤,则购进金梅弥猴桃(1000y)斤,根据总利润=每斤的利润×销售数量,即可得出关于y的一元一次方程,解之即可得出y值,进而可得出今年九月上半月购进普通猴桃及金梅弥猴桃的数量,再由总利润=每斤的利润×销售数量结合下半月获利比上半月的2倍少400元,即可得出关于a的一元二次方程,解之取其正值即可得出结论.
解:(1)设购进金梅弥猴桃x斤,则购进普通弥猴桃(900x)斤,
根据题意得:10x+3(900x)≤6200,
解得:x≤500.
答:金梅弥猴桃最多能购进500斤;
(2)设该超市今年九月上半月购进普通弥猴桃y斤,则购进金梅弥猴桃(1000y)斤,
根据题意得:(83)y+(1610+4)(1000y)=8000,
解得:y=400,
∴1000y=600.
∵下半月获利比上半月的2倍少400元,
∴[8(1a%)3]×400+[16(1+2a%)10+4]×600(1+![]() %)=8000×2400,
%)=8000×2400,
整理得:4a2+375a11875=0,
解得:a1=25,a2=![]() (舍去).
(舍去).
答:a的值为25.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
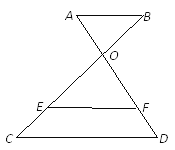
【题目】如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
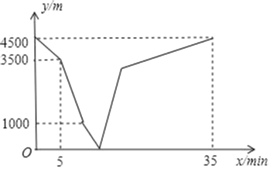
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
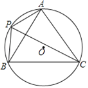
【题目】如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
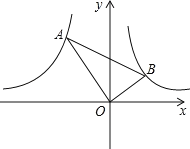
【题目】如图,已知点A,B分别是反比例函数y![]() (x<0),y
(x<0),y![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO![]() ,则k的值为_________.
,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑“是中考体育必考项目之一,某中学为了了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑时间长短依次分为A、B、C、D四个等级进行统计,制作出如下两个不完整的统计图.
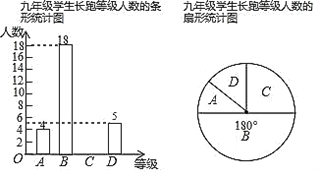
根据所给信息,解答下列问题:
(1)在扇形统计用中,C对应的扇形圆心角是____度.
(2)补全条形统计图.
(3)所抽取学生的“长跑”测试成绩的中位数会落在_____等级.
(4)该校九年有486名学生,请估计“长跑”测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).

A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com