
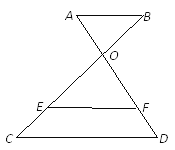
【题目】如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣5x+5与x轴、y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴交于另一点B.
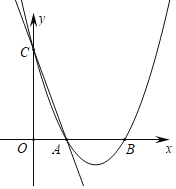
(1)求抛物线解析式及B点坐标;
(2)x2+bx+c≥﹣5x+5的解集 .
(3)若点M在第一象限内抛物线上一动点,连接MA、MB,当点M运动到某一位置时,△ABM面积为△ABC的面积的![]() 倍,求此时点M的坐标.
倍,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
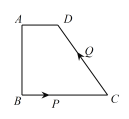
【题目】如图,四边形 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点 ![]() 从点
从点 ![]() 出发以
出发以 ![]() 的速度沿
的速度沿 ![]() 的方向运动,动点
的方向运动,动点 ![]() 从点
从点 ![]() 出发以
出发以 ![]() 的速度沿
的速度沿 ![]() 方向运动,
方向运动,![]() ,
,![]() 两点同时出发,当
两点同时出发,当 ![]() 到达点
到达点 ![]() 时停止运动,点
时停止运动,点 ![]() 也随之停止,设运动的时间为
也随之停止,设运动的时间为 ![]() .
.
(1)求线段 ![]() 的长;
的长;
(2)![]() 为何值时,线段
为何值时,线段 ![]() 将四边形
将四边形 ![]() 的面积分为
的面积分为 ![]() 两部分.
两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作试验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为8的正方形ABCD中,点P在BC边上,CP=2,点Q为线段AP上一动点,射线BQ与正方形ABCD的一边交于点R,且AP=BR,那么![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九月份,开州本地弥猴桃全面上市,其中新品种金梅弥猴桃因其个大多汁而深受大家喜爱,但弥猴桃一直因保鲜技术问题销售量不多,今年终于突破保鲜技术,水果售量明显上升.永辉超市准备大量进货,已知去年同期普通弥猴桃进价3元/斤,金梅弥猴桃进价10元/斤,去年九月共进货900斤.
(1)若去年九月两种弥猴桃进货总价不超过6200元,则金梅弥猴桃最多能购进多少斤?
(2)若永辉超市今年九月上半月共购进1000斤弥猴桃,其中普通弥猴桃进价与去年相同,金梅弥猴桃进价降4元,结果普通弥猴桃按8元/斤,金梅弥猴桃按16元/斤的价格卖出后共获利8000元,下半月因临近祖国七十华诞,水果需量上升,两种弥猴桃进价在上半月基础上保持不变,售价一路上涨,超市调整计划,普通弥猴桃进货量与上半月持平,售价下降a%吸引顾客;金梅弥猴桃进货量上涨生![]() %,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
%,售价上涨2a%,最后截至九月底,下半月获利比上半月的2倍少400元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
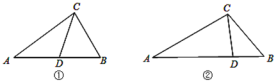
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的不断提高,越来越多的人选择到电影院观看电影,体验视觉盛宴,并且更多的人通过网上平台购票,既快捷又能享受更多优惠.某电影城2019年从网上购买![]() 张电影票的费用比现场购买
张电影票的费用比现场购买![]() 张电影票的费用少
张电影票的费用少![]() 元:从网上购买
元:从网上购买![]() 张电影票的费用和现场购买
张电影票的费用和现场购买![]() 张电影票的费用共
张电影票的费用共![]() 元.
元.
(1)求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
(2)2019年五一当天,该电影城按照2019年网上购票和现场购票的价格销售电影票,当天售出的总票数为![]() 张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低
张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低![]() 元,售出总票数就比五一当天增加
元,售出总票数就比五一当天增加![]() 张.经统计,5月5日售出的总票数中有
张.经统计,5月5日售出的总票数中有![]() 的电影票通过网上售出,其余通过现场售出,且当天票房总收入为
的电影票通过网上售出,其余通过现场售出,且当天票房总收入为![]() 元,试求出5月5日当天现场购票每张电影票的价格为多少元?
元,试求出5月5日当天现场购票每张电影票的价格为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com