
【题目】边长为8的正方形ABCD中,点P在BC边上,CP=2,点Q为线段AP上一动点,射线BQ与正方形ABCD的一边交于点R,且AP=BR,那么![]() ____________
____________
【答案】![]() 或1
或1
【解析】
分两种情形:①当R在AD边上时,易得△AQR∽△PQB且相似比为1:1,从而得解;②当R在CD上时,先证明BR⊥AP,再根据等面积法计算BQ,根据线段的和差计算QR,计算比值即可得解.
①当R在AD边上时,
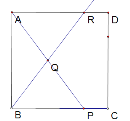
∵四边形ABCD为正方形
∴∠BAR=∠ABP=90°,AR∥BP
又∵AP=BR,AB=AB,
∴△ABP≌△BAR,
∴AR=BP,
∵AR∥BP,
∴△AQR∽△PQB
∴![]() .
.
②当R在CD上时,
∵四边形ABCD为正方形
∴∠ABC=∠BCR=90°,AB=BC
又∵AP=BR
∴△ABP≌△BCR,
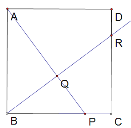
∴∠BAP=∠CBR,
∵∠CBR+∠ABR=90°,
∴∠BAP+∠ABR=90°,
∴∠AQB=90°,
∴BR⊥AP,
∵AB=8.BP=6,
∴AP=BR=![]() ,
,
∵![]() ABBP=
ABBP=![]() APBQ,
APBQ,
∴![]() ,
,
∴![]()
故答案为1或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在4×4的网格中,每一个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,以O为坐标原点建立如图所示的平面直角坐标系.若抛物线y=x2+bx+c的图象至少经过图中(4×4的网格中)的三个格点,并且至少一个格点在x轴上,则符合要求的抛物线一定不经过的格点坐标为( )
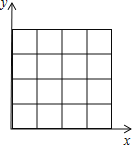
A.(1,3)B.(2,3)C.(1,4)D.(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
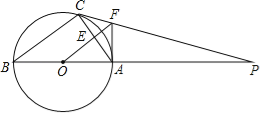
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
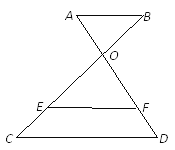
【题目】如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
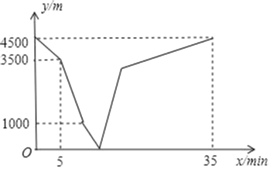
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
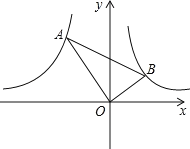
【题目】如图,已知点A,B分别是反比例函数y![]() (x<0),y
(x<0),y![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO![]() ,则k的值为_________.
,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com