
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
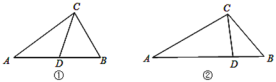
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据三角形内角和定理求出∠ACB=80°,根据角平分线的定义得到∠ACD=40°,证明△BCD∽△BAC,即可得到结论;
(2)根据完美分割线的定义,以及△ACD是以CD为底边的等腰三角形,得到△BCD∽△BAC,从而![]() ,设BD=x,解方程求出x,根据相似三角形的性质定理列式计算即可.
,设BD=x,解方程求出x,根据相似三角形的性质定理列式计算即可.
(1)∵∠A=40°,∠B=60°,∴∠ACB=80°,∴△ABC不是等腰三角形.
∵CD平分∠ACB,∴∠ACD=∠BCD![]() ∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD是等腰三角形.
∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD是等腰三角形.
∵∠BCD=∠A=40°,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD是△ABC的完美分割线;
(2)∵CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,∴△BCD∽△BAC,∴![]() .
.
∵AC=AD=2,BC![]() ,设BD=x,则AB=4+x,∴
,设BD=x,则AB=4+x,∴![]() ,解得:x=﹣1±
,解得:x=﹣1±![]() .
.
∵x>0,∴BD=x=﹣1![]() .
.
∵△BCD∽△BAC,∴![]() .
.
∵AC=2,BC![]() ,BD=﹣1
,BD=﹣1![]() ,∴CD
,∴CD![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】每年的9月3日是中国人民抗日战争胜利纪念日,某红色旅游景区为纪念抗日战争胜利73周年,今年9~10月份,对团体购买门票实行优惠,决定在原定票价基础上每张降价16元,这样按原定票价需花费2000元购买的门票张数,现在只花费了1200元.
(1)求每张门票的原定票价;
(2)根据实际情况,该景区决定对网上购票的个人也采取优惠,原定票价经过连续两次降价后票价为每张32.4元,求原定票价平均每次的下降率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
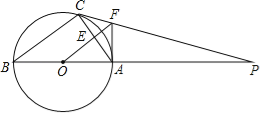
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
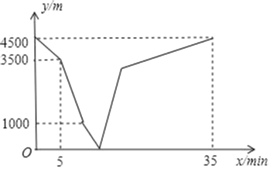
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是
与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是![]() ,过点F作直线FG//BC交x轴于点G.
,过点F作直线FG//BC交x轴于点G.
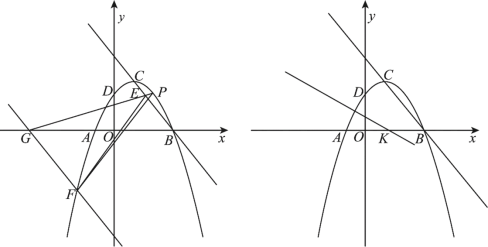
(1)点P是直线BC上方抛物线上的一动点,连接PG与直线BC交于点E,连接EF,PF,当![]() 的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
(2)如图2,连接AD,作AD的垂直平分线与x轴交于点K,平移抛物线,使抛物线的顶点C在射线BC上移动,平移的距离是t,平移后抛物线上点A,点C的对应点分别为点A′,点C′,连接A′C′,A′K,C′K,![]() A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
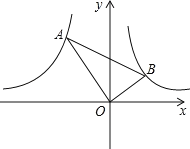
【题目】如图,已知点A,B分别是反比例函数y![]() (x<0),y
(x<0),y![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO![]() ,则k的值为_________.
,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2+bx+c经过(﹣3,0),(1,0)两点
(1)求抛物线的解析式,并求出其开口方向和对称轴
(2)用配方法求出该抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
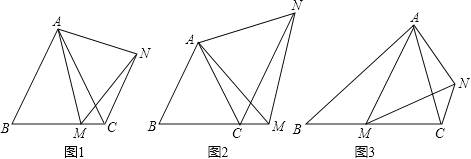
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
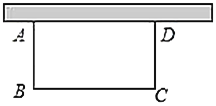
【题目】如图,用一段长为![]() 的篱笆围成一个一边靠墙的矩形花圃
的篱笆围成一个一边靠墙的矩形花圃![]() ,墙长
,墙长![]() .设
.设![]() 长为
长为![]() ,矩形的面积为
,矩形的面积为![]() .
.
(1)写出![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 长为多少米时,所围成的花圃面积最大?最大值是多少?
长为多少米时,所围成的花圃面积最大?最大值是多少?
(2)当花圃的面积为![]() 时,
时,![]() 长为多少米?
长为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com