
【题目】如图1,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是
与x轴交于A,B两点(点A在点B左侧),与y轴交于点D,点C为抛物线的顶点,过B,C两点作直线BC,抛物线上的一点F的横坐标是![]() ,过点F作直线FG//BC交x轴于点G.
,过点F作直线FG//BC交x轴于点G.
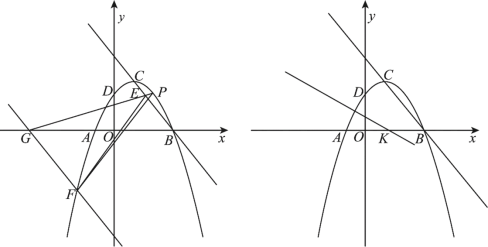
(1)点P是直线BC上方抛物线上的一动点,连接PG与直线BC交于点E,连接EF,PF,当![]() 的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
的面积最大时,在x轴上有一点R,使PR+CR的值最小,求出点R的坐标,并直接写出PR+CR的最小值;
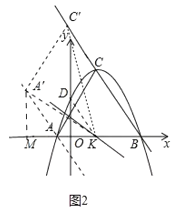
(2)如图2,连接AD,作AD的垂直平分线与x轴交于点K,平移抛物线,使抛物线的顶点C在射线BC上移动,平移的距离是t,平移后抛物线上点A,点C的对应点分别为点A′,点C′,连接A′C′,A′K,C′K,![]() A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
A′C′K是否能为等腰三角形?若能,求出t的值;若不能,请说明理由.
【答案】(1)点R坐标为(![]() ,0),
,0),![]() ;(2)存在,t的值为
;(2)存在,t的值为![]() 或
或![]() .
.
【解析】
(1)首先求出B、C两点坐标,即可确定直线BC的解析式,求出FG的解析式即可求出点G的坐标,如图1中,过点G作y轴的平行线,过F作x轴的平行线交于点K,连接PK.设P(m,![]() ),因为BC∥FG,FG是定值,所以△EFG的面积是定值,所以△PFG的面积最大时,△PEF的面积最大,构建二次函数,利用二次函数的性质求出点P坐标,作P关于x轴的对称点P′,连接P′C交x轴于R,此时CR+RP最小,由此即可解决问题.
),因为BC∥FG,FG是定值,所以△EFG的面积是定值,所以△PFG的面积最大时,△PEF的面积最大,构建二次函数,利用二次函数的性质求出点P坐标,作P关于x轴的对称点P′,连接P′C交x轴于R,此时CR+RP最小,由此即可解决问题.
(2)分三种情形讨论即可:①当KA′=A′C′时,②当C′A′=C′K时,③当KA′=KC′时,分别列出方程求解即可.
解:(1)对于抛物线![]() ,另y=0得到
,另y=0得到![]() ,
,
解得:![]() 或
或![]() ,
,
∴点B坐标为(![]() ,0),
,0),
∵![]() ,
,
∴顶点C的坐标为:(![]() ,4),
,4),
设直线BC解析式为y=kx+b,
则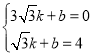 ,解得:
,解得: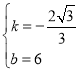 ,
,
∴直线BC解析式为:![]() ,
,
将F的横坐标代入抛物线解析式可得:F(![]() ,-5),
,-5),
∵FG//BC,
∴直线FG解析式为:![]() ,
,
令y=0得到![]() ,
,
∴点G坐标为:(![]() ),
),
如图1中,过点G作y轴的平行线,过F作x轴的平行线交于点K,连接PK.
设P(m,![]() ),
),
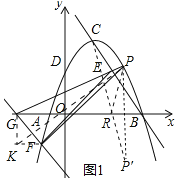
∵BC∥FG,FG是定值,
∴△EFG的面积是定值,
∴△PFG的面积最大时,△PEF的面积最大,
∵S△PFG=S△PGK+S△PFK-S△FGK=![]()
![]() ,
,
∵![]() <0,
<0,
∴m=![]() 时,△PFG的面积最大,即△PEF的面积最大,
时,△PFG的面积最大,即△PEF的面积最大,
∴P(![]() ,3),
,3),
作P关于x轴的对称点P′(![]() ,-3),连接P′C交x轴于R,此时CR+RP最小,
,-3),连接P′C交x轴于R,此时CR+RP最小,
最小值=CP′=![]() ,
,
设直线P′C的解析式为:![]() ,
,
则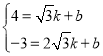 ,解得:
,解得: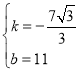
∴直线P′C的解析式为![]() ,
,
当y=0时,![]() ,
,
∴点R坐标为(![]() ,0);
,0);
(2)如图2中,连接DK,DA,
∵A(![]() ),D(0,3),
),D(0,3),
∴OA=![]() ,DO=3,
,DO=3,
∴tan∠DAO=![]() ,
,
∴∠DAO=60°,
∵KA=KD,
∴△ADK是等边三角形,
∴AD=AK=![]() ,K(
,K(![]() ,
,
①∵A(![]() ,0),C(
,0),C(![]() ,4),
,4),
∴AC=![]() ,
,
当KA′=A′C′=AC=![]() 时,
时,
∵AA′=t,tan∠A′AM=tan∠ABC=![]() ,
,
∴sin∠A′AM=sin∠ABC=![]() ,
,
∴A′M=![]() ,AM=
,AM=![]() ,
,
在Rt△A′MK中,A′K2=A′M2+KM2=![]() +(
+(![]() )2,
)2,
∴![]() +(
+(![]() )2=(
)2=(![]() )2,
)2,
解得:![]() 或
或![]() (舍去);
(舍去);
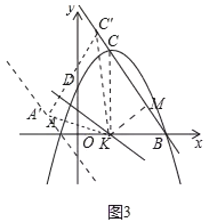
②如图3,当C′A′= C′K时,连接CK,作KM⊥BC于M,
在Rt△BCK中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴C′K2=KM2+ C′M2=![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
③当KA′= KC′时,![]() +(
+(![]() )2=
)2=![]() ,
,
解得:![]() (舍去),
(舍去),
综上所述,当△A′C′K为等腰三角形时,t的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AD是Rt△ABC斜边BC上的中线,过A,D两点的⊙O交AC于E,弦EF∥BC.
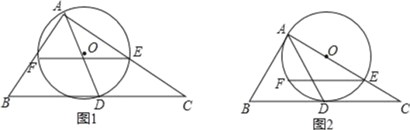
(1)求证:AD=EF;
(2)若O在AC边上,且⊙O与BC边相切,当EF=2时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数![]() 、
、![]() 、
、![]() ,用
,用![]() 表示这三个数的中位数,用
表示这三个数的中位数,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]() ,
,![]() .
.
解决问题:
(1)填空:如果![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
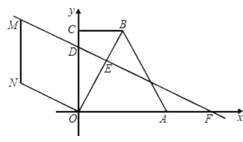
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() 边所在直线为
边所在直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求点![]() 的坐标;
的坐标;
(2)已知![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点E作EG⊥x轴于G,且EG:OG=2.求直线
,过点E作EG⊥x轴于G,且EG:OG=2.求直线![]() 的解析式;
的解析式;
(3)点![]() 是(2)中直线
是(2)中直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上方的平面内是否存在一点
轴上方的平面内是否存在一点![]() ,使以
,使以![]() 为顶点的四边形为菱形?若存在,请求出
为顶点的四边形为菱形?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
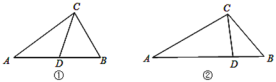
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
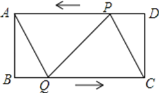
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD(AD>AB)沿BD折叠,点C落在点C′处.
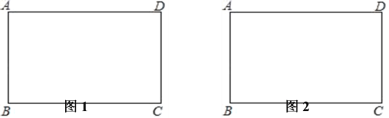
(1)连接BD,请用直尺和圆规在图1中作出点C′;(不写作法,保留作图痕迹)
(2)若BC′与AD相交于点E,EB与ED的数量关系是 ;连接AC′,则AC′与BD的位置关系是 ;
(3)在(2)的条件下,若AB=4,AD=8,求BE的长.(提示:(2)、(3)两题可以在图2中作出草图完成)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,加速了快递行业的发展,据调查,某家小型快递公司,今年3月与5月完成投递的快件总数分别为10万件和14.4万件,现假定该公司每月投递的快件总数的增长率相同.
(1)求该快递公司投递快件总数的月平均增长率?
(2)如果该公司平均每名快件投递业务员每月最多可投递快件0.6万件,那么该公司现有的21名快件投递业务员能否完成今年6月的快件投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com