
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ķ�չ���ݵ��飬ij��С�Ϳ�ݹ�˾������3����5�����Ͷ�ݵĿ�������ֱ�Ϊ10�����14.4������ּٶ��ù�˾ÿ��Ͷ�ݵĿ����������������ͬ.
(1)��ÿ�ݹ�˾Ͷ�ݿ����������ƽ�������ʣ�
(2)����ù�˾ƽ��ÿ�����Ͷ��ҵ��Աÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ���ɽ���6�µĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
���𰸡�(1)![]() ��(2)������Ҫ����8��ҵ��Ա.
��(2)������Ҫ����8��ҵ��Ա.
��������
(1)��ÿ�ݹ�˾Ͷ���ܼ�������ƽ��������Ϊx�����ݡ�����1�·���3�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����14.4������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ���������̣��ⷽ�̼��ɣ�
��2����������������·ݵĿ��Ͷ�����������26�����Ͷ��ҵ��Ա����ɵĿ��Ͷ�����Ƚϵó��ù�˾������ɽ���4�·ݵĿ�����������������Ҫ����ҵ��Ա������.
(1)�⣺����ƽ��������Ϊ![]() ������ã�
������ã�![]()
���![]() ��
��![]() (��ȥ)
(��ȥ)
����ƽ��������Ϊ![]() .
.
(2)![]() (���)
(���)
![]() (���)
(���)
��![]()
��������ɽ���6�µĿ��Ͷ�ݷ���.
![]()
��������Ҫ����8��ҵ��Ա.


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�D����CΪ�����ߵĶ��㣬��B��C������ֱ��BC���������ϵ�һ��F�ĺ�������
��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�D����CΪ�����ߵĶ��㣬��B��C������ֱ��BC���������ϵ�һ��F�ĺ�������![]() ������F��ֱ��FG//BC��x���ڵ�G.
������F��ֱ��FG//BC��x���ڵ�G.
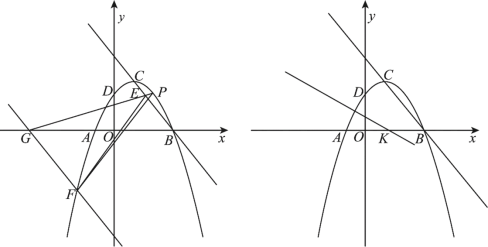
��1����P��ֱ��BC�Ϸ��������ϵ�һ���㣬����PG��ֱ��BC���ڵ�E������EF��PF����![]() ��������ʱ����x������һ��R��ʹPR+CR��ֵ��С�������R�����꣬��ֱ��д��PR+CR����Сֵ��
��������ʱ����x������һ��R��ʹPR+CR��ֵ��С�������R�����꣬��ֱ��д��PR+CR����Сֵ��
��2����ͼ2������AD����AD�Ĵ�ֱƽ������x�ύ�ڵ�K��ƽ�������ߣ�ʹ�����ߵĶ���C������BC���ƶ���ƽ�Ƶľ�����t��ƽ�ƺ��������ϵ�A����C�Ķ�Ӧ��ֱ�Ϊ��A������C��������A��C����A��K��C��K��![]() A��C��K�Ƿ���Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵������.
A��C��K�Ƿ���Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽƬABCD��AB=9��BC=6���ھ��α�����һ��P����DP=3��������ֽƬ�۵���ʹ��B���P�غϣ��ۺ�����ֱ�߽����������ڵ�E��F����EF��Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
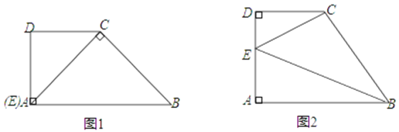
��1������![]() ��
��![]() ǡ���غ�ʱ����ͼ1������
ǡ���غ�ʱ����ͼ1������![]() �ij���
�ij���
��2���ʣ��Ƿ����ʹ![]() ��
��![]() ��
��![]() �����ƣ����ܣ��������ʱ
�����ƣ����ܣ��������ʱ![]() �ij��������ܣ���˵�����ɣ���ͼ2����
�ij��������ܣ���˵�����ɣ���ͼ2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����飬ij����Ʒ�ڵ�x����ۼ��������������Ϣ���±�����֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒÿ�������ΪyԪ��

��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
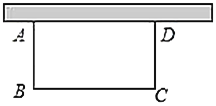
����Ŀ����ͼ����һ�γ�Ϊ![]() �����Χ��һ��һ�߿�ǽ�ľ��λ���
�����Χ��һ��һ�߿�ǽ�ľ��λ���![]() ��ǽ��
��ǽ��![]() ����
����![]() ��Ϊ
��Ϊ![]() �����ε����Ϊ
�����ε����Ϊ![]() ��
��
��1���![]() ��
��![]() �ĺ�����ϵʽ����
�ĺ�����ϵʽ����![]() ��Ϊ������ʱ����Χ�ɵĻ������������ֵ�Ƕ��٣�
��Ϊ������ʱ����Χ�ɵĻ������������ֵ�Ƕ��٣�
��2�������Ե����Ϊ![]() ʱ��
ʱ��![]() ��Ϊ�����ף�
��Ϊ�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC���е�ΪO����G��H�ڶԽ���AC�ϣ�AG��CH��ֱ��GH�Ƶ�O��ʱ����ת���ǣ����AB��CD�ֱ��ཻ�ڵ�E��F����E�����A��B�غϣ���
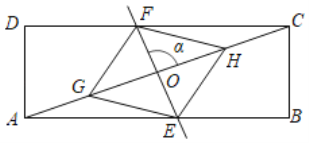
��1����֤���ı���EHFG��ƽ���ı��Σ�
��2����������90����AB��9��AD��3����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
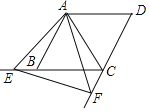
����Ŀ����ͼ��������![]() �У���֪
�У���֪![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() ���ӳ����ϣ������н��ۣ���
���ӳ����ϣ������н��ۣ���![]() ����
����![]() ����
����![]() ������
������![]() �����
�����![]() ��
��![]() �ľ���Ϊ
�ľ���Ϊ![]() ����������ȷ���۵ĸ�����( )
����������ȷ���۵ĸ�����( )
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c�Ķ���ΪD����1��2������x���һ������A�ڵ㣨��3��0���ͣ���2��0��֮�䣬�䲿��ͼ����ͼ�������½��ۣ���b2��4ac��0���ڵ�x����1ʱ��y��x�������С����a+b+c��0����������ax2+bx+c��m=0û��ʵ��������m��2������3a+c��0��������ȷ���۵ĸ����ǣ�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com