
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
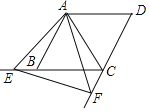
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①只要证明![]() 即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点
即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点![]() 到
到![]() 的距离即可判断.综上即可得答案.
的距离即可判断.综上即可得答案.
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∵∠ABC=60°,
∴![]() 是等边三角形,
是等边三角形,
∴∠ACD=∠ACB=60°,AB=AC,
∴∠ABE=∠ACF=120°,
∵![]() ,
,
∴∠BAE+∠BAF=∠CAF+∠BAF=60°,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,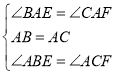 ,
,
∴![]() ,
,
∴![]() ,
,![]() .故①正确;
.故①正确;
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故②正确;
,故②正确;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 和
和![]() 不会相似,故③不正确;
不会相似,故③不正确;
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴点![]() 到
到![]() 的距离为
的距离为![]() ,故④不正确.
,故④不正确.
综上,正确结论有①②,共2个,
故选B.



科目:初中数学 来源: 题型:
【题目】如图,图![]() 正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
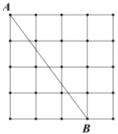
(1)在图中画出一个直角![]() ,并且其面积为5;
,并且其面积为5;
(2)在图中画出一个等腰直角![]() ;
;
(3)连接![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作(九章算术)中有如下问题:“今有人持金出五关,前关二而税一.次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.”其意思为“今有人持金出五关,第![]() 关所收税金为持金的
关所收税金为持金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,
,![]() 关所收税金之和,恰好重
关所收税金之和,恰好重![]() 斤.”若设这个人原本持金
斤.”若设这个人原本持金![]() 斤,根据题意可列方程为__________ .
斤,根据题意可列方程为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图①,以直角三角形的各边为边向外作等边三角形,再把较小的两个等边三角形按如图②的方式放置在最大等边三角形内.若知道图②中阴影部分的面积,则一定能求出图②中( )
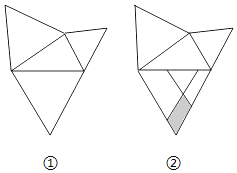
A.最大等边三角形与直角三角形面积的和B.最大等边三角形的面积
C.较小两个等边三角形重叠部分的面积D.直角三角形的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积和气体对汽缸壁所产生的压强.
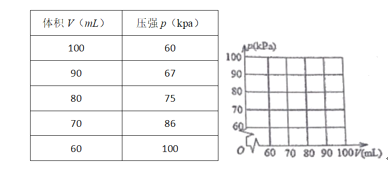
(1)根据表中的数据画出函数图像,并求出压强p(kpa)关于体积V(mL)的函数表达式;
(2)当压力表读出的压强为72kpa时,汽缸内气体的体积压缩到多少毫升?
(3)若压强80<p<90,估计气缸内气体体积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:(1)如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2),请你写出![]() 、
、![]() 、ab之间的等量关系是______________;
、ab之间的等量关系是______________;
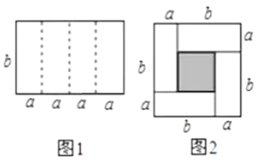
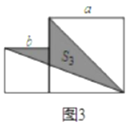
(2)两个边长分别为a和b的正方形如图放置(图3),求出图3中阴影部分的面积![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,连接AD,E为AD的中点,过A作AF∥BC交BE延长线于F,连接CF.
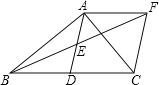
(1)求证:四边形ADCF是菱形;
(2)在不添加任何辅助线的情况下,请直接写出与△ACD面积相等的三角形(不包含△ACD).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个几何体的俯视图,则这个几何体的形状可能是( )
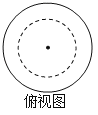
A.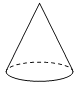 B.[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/21/2489183741517824/2490750925307904/STEM/789274b5f2a548a49af6fc88629e8cdc.png] C.
B.[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/21/2489183741517824/2490750925307904/STEM/789274b5f2a548a49af6fc88629e8cdc.png] C.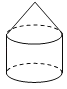 D.
D.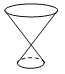
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com