
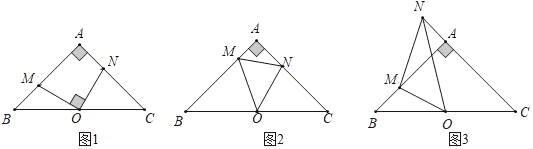
【题目】在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.
(1)如图1,当α=90°时,求证:AM=CN;
(2)如图2,当α=45°时,问线段BM、MN、AN之间有何数量关系,并证明;
(3)如图3,当α=45°时,旋转∠MON,问线段之间BM、MN、AN有何数量关系?并证明.
【答案】(1)证明见解析;(2)BM=AN+MN,理由见解析;(3)MN=AN+BM.理由见解析.
【解析】
(1)根据题意AB=AC,∠BAC=90°,得出![]() 是一个等腰直角三角形,再根据三线合一得出OA=OB=OC,从而∠ABO=∠ACO=∠BAO=∠CAO=45°,且AO⊥BC,从而得出∠MON=∠AOC=90°,再又因为等角的余角相等,所以∠AOM=∠CON,所以通过证明△AOM≌△CON得出AM=CN
是一个等腰直角三角形,再根据三线合一得出OA=OB=OC,从而∠ABO=∠ACO=∠BAO=∠CAO=45°,且AO⊥BC,从而得出∠MON=∠AOC=90°,再又因为等角的余角相等,所以∠AOM=∠CON,所以通过证明△AOM≌△CON得出AM=CN
(2)根据题意,在BA上截取BG=AN,连接GO,AO,先证明△BGO≌△AON,再证明△GMO≌△NMO得出GM=MN,从而证明出BM=AN+MN
(3)根据题意,过点O作OG⊥ON,连接AO,先证明△NAO≌△GBO,得到AN=
GB,GO=ON,再证明△MON≌△MOG得到MN=MG,从而进一步证明出MN=AN+BM
证明:(1)如图1,连接OA,

∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∴∠MON=∠AOC=90°,
∴∠AOM=∠CON,且AO=CO,∠BAO=∠ACO=45°,
∴△AOM≌△CON(ASA)
∴AM=CN;
(2)BM=AN+MN,
理由如下:如图2,在BA上截取BG=AN,连接GO,AO,
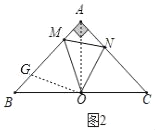
∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∵BG=AN,∠ABO=∠NAO=45°,AO=BO,
∴△BGO≌△AON(SAS)
∴OG=ON,∠BOG=∠AON,
∵∠MON=45°=∠AOM+∠AON,
∴∠AOM+∠BOG=45°,且∠AOB=90°,
∴∠MOG=∠MON=45°,且MO=MO,GO=NO,
∴△GMO≌△NMO(SAS)
∴GM=MN,
∴BM=BG+GM=AN+MN;
(3)MN=AN+BM,
理由如下:如图3,过点O作OG⊥ON,连接AO,
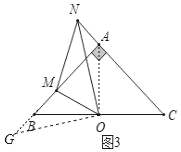
∵AB=AC,∠BAC=90°,OB=OC,
∴AO⊥BC,OA=OB=OC,∠ABO=∠ACO=∠BAO=∠CAO=45°,
∴∠GBO=∠NAO=135°,
∵MO⊥GO,
∴∠NOG=90°=∠AOB,
∴∠BOG=∠AON,且AO=BO,∠NAO=∠GBO,
∴△NAO≌△GBO(ASA)
∴AN=GB,GO=ON,
∵MO=MO,∠MON=∠GOM=45°,GO=NO,
∴△MON≌△MOG(SAS)
∴MN=MG,
∵MG=MB+BG,
∴MN=AN+BM.


科目:初中数学 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大美开州,最帅汉丰湖,汉丰湖步道已成为市民最好休闲圣地.雪松和余乐乐相约分别从举子园、博物馆出发,沿环湖步道相向而行.雪松开始跑步前进,中途在某地改为步行,且步行的速度为跑步速度的一半,雪松先出发5分钟后,余乐乐才骑自行车匀速向举子园行驶.雪松到达博物馆恰好用了35分钟.两人之间的距离y(m)与雪松离开出发地的时间x(min)之间的函数图象如图所示,则当余乐乐刚到举子园时,雪松离举子园的距离为_____米.
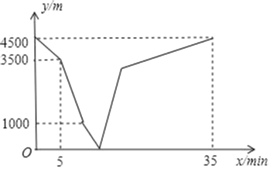
查看答案和解析>>
科目:初中数学 来源: 题型:
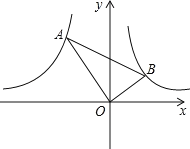
【题目】如图,已知点A,B分别是反比例函数y![]() (x<0),y
(x<0),y![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO![]() ,则k的值为_________.
,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=2x2+bx+c经过(﹣3,0),(1,0)两点
(1)求抛物线的解析式,并求出其开口方向和对称轴
(2)用配方法求出该抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“长跑“是中考体育必考项目之一,某中学为了了解九年级学生“长跑”的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑时间长短依次分为A、B、C、D四个等级进行统计,制作出如下两个不完整的统计图.
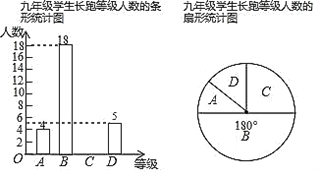
根据所给信息,解答下列问题:
(1)在扇形统计用中,C对应的扇形圆心角是____度.
(2)补全条形统计图.
(3)所抽取学生的“长跑”测试成绩的中位数会落在_____等级.
(4)该校九年有486名学生,请估计“长跑”测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
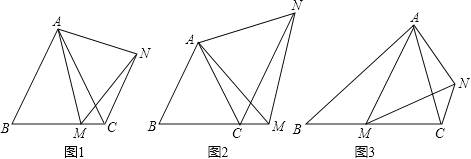
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com