
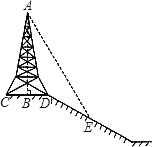
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=20m,DE=30m,小明和小华的身高都是1.5m,同一时刻,小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是_____米.
【答案】37.5
【解析】
仔细观察图形,理解铁塔AB的影子是由坡面DE与平地BD两部分组成.
塔影落在坡面部分的塔高:塔影DE长=小明的身高:小明的影长;
塔影落在平地部分的塔高:塔影BD长=小华的身高:小华的影长.
设塔影留在坡面DE部分的塔高为h1、塔影留在平地BD部分的塔高为h2,则铁塔的高为h1+h2.
解:过D点作DF∥AE,交AB于F点,如图所示: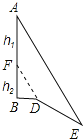
设塔影留在坡面DE部分的塔高AF=h1、塔影留在平地BD部分的塔高BF=h2,
则铁塔的高为h1+h2.
∵h1:30m=1.5m:2m,
∴h1=22.5m;
∵h2:10m=1.5m:1 m,
∴h2=15m.
∴AB=22.5+15=37.5(m).
∴铁塔的高度为37.5m.
故答案为:37.5.


科目:初中数学 来源: 题型:
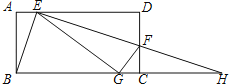
【题目】如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若![]() ,则
,则![]() .以上命题,正确的有( )
.以上命题,正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
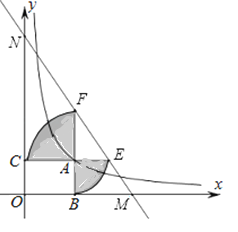
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆,售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元,每减少1盆,盆景的平均每盆利润增加2元;
②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加![]() 盆,第二期盆景与花卉售完后的利润分别为
盆,第二期盆景与花卉售完后的利润分别为![]() ,
,![]() (单位:元)
(单位:元)
(1)用含![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() .
.
(2)当![]() 取何值时,第二期培植的盆录与花卉售完后获得的总利润
取何值时,第二期培植的盆录与花卉售完后获得的总利润![]() 最大,最大总利润是多少?
最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是指空气中直径小于或等于
是指空气中直径小于或等于![]() 的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,
的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,

(1)2018年7~12月![]() 平均浓度的中位数为
平均浓度的中位数为 ![]() ;
;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映2018年7~12月![]() 平均浓度变化过程和趋势的统计图是 ;
平均浓度变化过程和趋势的统计图是 ;
(3)某同学观察统计表后说:“2018年7~12月与2017年同期相比,空气质量有所改善”,请你用一句话说明该同学得出这个结论的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“文化宜昌全民阅读”活动中,某中学社团“精一读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查,2012年全校有1000名学生,2013年全校学生人数比2012年增加10%,2014年全校学生人数比2013年增加100人.
(1)求2014年全校学生人数;
(2)2013年全校学生人均阅读量比2012年多1本,阅读总量比2012年增加1700本(注:阅读总量=人均阅读量×人数)
①求2012年全校学生人均阅读量;
②2012年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2012年、2014年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2014年全校学生人均阅读量比2012年增加的百分数也是a,那么2014年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.

(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .点
.点![]() 为
为![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 切
切![]() 于点
于点![]() ,设
,设![]() .
.
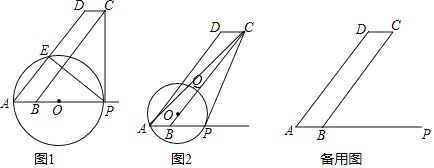
(1)如图1,![]() 为何值时,圆心
为何值时,圆心![]() 落在
落在![]() 上?若此时
上?若此时![]() 交
交![]() 于点
于点![]() ,直接指出PE与BC的位置关系;
,直接指出PE与BC的位置关系;
(2)当![]() 时,如图2,
时,如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数,并通过计算比较弦
的度数,并通过计算比较弦![]() 与劣弧
与劣弧![]() 长度的大小;
长度的大小;
(3)当![]() 与线段
与线段![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com