
����Ŀ��ijѧУΪ�˽ⱾУ���꼶ѧ����ĩ������ѧ����������������г�����������֪��У���꼶����10���࣬ÿ��40��ѧ���������Ҫ��ش��������⣺
��1����Ҫ��ȫ�꼶ѧ���г�ȡһ��40�˵�����������Ϊ���³��������бȽϺ��������� ������ֻҪ��д��ţ�
�������ȡһ���༶��ѧ��������ȫ�꼶ѧ���������ȡ40����ѧ��������ȫ�꼶10�����и������ȡ4��ѧ����
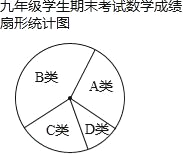
��2������ȡ��40��ѧ������ѧ�ɼ����з��飬������Ƶ�����ͳɷֲ�ͳ��ͼ���������������ͼ����C��D��Բ�ĽǶ����ֱ�Ϊ�� �����ڹ���ȫ�꼶A��B��ѧ��������Լ������ ����
�ɼ�����λ���֣� | Ƶ�� | Ƶ�� |
A�ࣨ80��100�� | 0.3 | |
B�ࣨ60��79�� | 0.4 | |
C�ࣨ40��59�� | 8 | |
D�ࣨ0��39�� | 4 |
��3��ѧУΪ�˽�����ѧУ��ѧ�ɼ��������ͬ��ε�GѧУ��JѧУ�ij������ݽ��жԱȣ����±�������Ϊ����ѧУ��ѧЧ���Ϻã�˵��������ɣ�
ѧУ | ƽ�������֣� | ���� | A��B��Ƶ�ʺ� |
GѧУ | 87 | 520 | 0.7 |
JѧУ | 87 | 478 | 0.65 |
���𰸡���1��������2��72�㡢36�㣻��280������3��GѧУ��ѧЧ���Ϻã����ɼ�����.
��������
��1�����ݳ�������ĺ����Խ����жϼ��ɵã�
��2������360�ȷֱ����C ��D��ռ�ı������ɵã�
����ȫ�꼶����������A��B���Ƶ�ʺͼ��ɵã�
��3������ͨ���߷�������Ƶ�ʵȷ�����бȽϣ�ֻҪ�������ɣ����ɵ�.
��1��������ɵã�
��Ҫ��ȫ�꼶ѧ���г�ȡһ��40�˵���������ȫ�꼶10�����и������ȡ4��ѧ���ȽϺ�����
�ʴ�Ϊ������
��2����C��Բ�ĽǶ���Ϊ��360���![]() =72�㣬D��Բ�ĽǶ���Ϊ��360���
=72�㣬D��Բ�ĽǶ���Ϊ��360���![]() =36�㣬
=36�㣬
�ʴ�Ϊ��72�㡢36�㣻
�ڹ���ȫ�꼶A��B��ѧ��������Լ���У�400����0.3+0.4��=280���ˣ���
�ʴ�Ϊ��280�ˣ�
��3��GѧУ��ѧЧ���Ϻã�
���ɣ���ΪA��B����Ƶ��֮��GѧУ����JѧУ������Ը߷�����GѧУ����JѧУ������GѧУ��ѧЧ���Ϻã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC������C=90������D��BC�ߵ��е���BD=2��tanB=![]() ��
��
��1����AD��AB�ij���
��2����sin��BAD��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
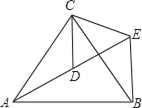
����Ŀ����ͼ����ACB����ECD���ǵȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��1����֤��AD=BE��
��2�����AEB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���һ���߶�AB����֪��A����3��0����B��0��4����ƽ���߶�AB�õ��߶�A1B1������A�Ķ�Ӧ��A1������Ϊ��0����1�������߶�ABƽ�ƾ����������ı���ABB1A1�������Ϊ��������
A. 12 B. 15 C. 24 D. 30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�����E��A��������A��B��C�����˶�������E�����Cʱֹͣ�˶�������E��EF��AE��CD�ڵ�F�����E�˶�·��Ϊx��CF=y����ͼ2����ʾ����y��x�ĺ�����ϵ�Ĵ���ͼ�������н��ۣ���a=3���ڵ�CF=![]() ʱ����E���˶�·��Ϊ
ʱ����E���˶�·��Ϊ![]() ��
��![]() ��
��![]() ���������ж���ȷ���ǣ�������
���������ж���ȷ���ǣ�������
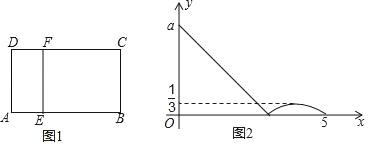
A. �٢ڶ��� B. �٢ڶ��� C. �ٶԢڴ� D. �ٴ��ڶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߳�Ϊa��������ABCD�У���E��BD��һ�㣬����E��EF��AE������CB�ڵ�F������CE��
��1������F�ڱ�BC�ϣ���ͼ����
����֤��CE=EF��
����BC=2BF����DE�ij���
��2������F��CB�ӳ����ϣ�BC=2BF����ֱ��д��DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����
��1����֪���߳������������������Ҫ֪��ʲô����ô�������ߣ�
��2���⣺���� ��������������ACD��ABD�ı�֮����ʲô��Ҫ��ϵ��
��3����BD��x���ֱ�������ֱ�����������ú�x��ʽ�ӱ�ʾAD2������ɽ�������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������е�ÿ��С�����α߳�����1����ͬѧ�����������߽��л�ͼ��
(1)��ͼ1�У���һ������Ϊ��㡢���Ϊ5�������Σ�
(2)��ͼ2�У���֪�߶�AB��CD�����߶�EF��ʹ����AB��CD�����Գ�ͼ�Σ�(Ҫ�����з���������߶�)
(3)��ͼ3�У���һ���D�����㣺����CB��CA�ľ�����ȣ�������A��C�ľ�����ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD=��CAE=90�㣬AB=AD��AE=AC��AF��CB������ΪF��
��1����֤����ABC�ա�ADE��
��2������FAE�Ķ�����
��3����֤��CD=2BF+DE��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com