
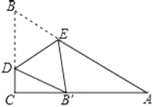
【题目】在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是________________.
【答案】3或3![]() -3或0
-3或0
【解析】
分三种情况讨论:当AB'=EB'时,△AEB′是等腰三角形;当AE=AB'时,△AEB′是等腰三角形;当AE=B'E时,△AEB′是等腰三角形,分别根据等腰三角形的性质以及勾股定理进行计算,即可得到CB′的值.
解:∵∠C=90°,∠A=30°,AB=6,
∴∠B=60°,BC=3,
分三种情况讨论:
①如图所示,当点D与点C重合时,∠B=∠CB'E=60°,
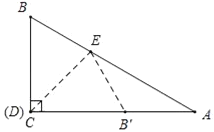
∵∠A=30°,
∴∠AEB'=30°,
∴∠A=∠AEB',
∴AB'=EB',即△AEB′是等腰三角形,
此时,CB'=BC=3;
②如图所示,当AE=AB'时,△AEB′是等腰三角形,
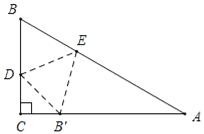
∴∠AB'E=75°,
由折叠可得,∠DB'E=∠ABC=60°,
∴∠DB'C=45°,
又∵∠C=90°,
∴△DCB'是等腰直角三角形,
设CB'=x=DC,则BD=3﹣x=DB',
∵Rt△DCB'中,x2+x2=(3﹣x)2,
解得x1=3![]() ﹣3,x2=﹣3
﹣3,x2=﹣3![]() ﹣3(舍去),
﹣3(舍去),
∴CB'=3![]() ﹣3;
﹣3;
③如图所示,当点B'与点C重合时,∠B=∠DCE=60°,

∴∠EB'A=30°=∠A,
∴AE=B'E,即△AEB′是等腰三角形,
此时CB'=0,
综上所述,当△AEB′是等腰三角形时,CB′的值是3或3![]() ﹣3或0.
﹣3或0.
故答案为:3或3![]() -3或0.
-3或0.


科目:初中数学 来源: 题型:
【题目】在一幅长60 cm、宽40 cm的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图.如果要使整个挂图的面积是2816 cm2,设金色纸边的宽为x cm,那么x满足的方程是( )

A. (60+2x)(40+2x)=2816
B. (60+x)(40+x)=2816
C. (60+2x)(40+x)=2816
D. (60+x)(40+2x)=2816
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“红灯停,绿灯行”是我们过路口遇见交通信号灯时必须遵守的规则.小明每天从家骑自行车上学要经过三个路口,假如每个路口交通信号灯中红灯和绿灯亮的时间相同,且每个路口的交通信号灯只安装了红灯和绿灯.那么某天小明从家骑车去学校上学,经过三个路口抬头看到交通信号灯.
(1)请画树状图,列举小明看到交通信号灯可能出现的所有情况;
(2)求小明途经三个路口都遇到红灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.
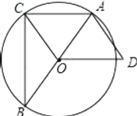
(1)当∠B=30°时,请判断四边形OCAD的形状,为什么?
(2)当∠B等于多少度时,AD与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
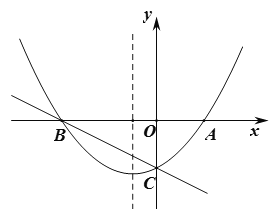
【题目】如图,对称轴是![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 若点
若点![]() 是直线
是直线![]() 下方的抛物线上的动点,求
下方的抛物线上的动点,求![]() 的面积的最大值;
的面积的最大值;
![]() 若点
若点![]() 在抛物线对称轴左侧的抛物线上运动,过点
在抛物线对称轴左侧的抛物线上运动,过点![]() 作
作![]() 铀于点
铀于点![]() ,交直线
,交直线![]() 于点
于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在对称轴上是否存在一点
在对称轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,请求出
的周长最小,若存在,请求出![]() 点的坐标和
点的坐标和![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com