
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是 (填编号)


②③
【考点】二次函数图象与系数的关系.
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解:根据图象知道
当x=1时,y=a+b+c>0,故①错误;
当x=﹣1时,y=a﹣b+c<0,故②正确;
∵抛物线开口朝下,
∴a<0,
∵对称轴x=﹣
 (0<x<1),
(0<x<1),
∴2a<﹣b,
∴b+2a<0,故③正确;
∵对称轴x=﹣
 (0<x<1),
(0<x<1),
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故④错误.
故答案为:②③.
【点评】此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用是解题关键.


科目:初中数学 来源: 题型:
如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1,则点A1的坐标为( )


A.(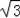
 ,1) B.(
,1) B.(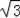
 ,﹣1) C.(1,﹣
,﹣1) C.(1,﹣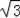
 ) D.(2,﹣1)
) D.(2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
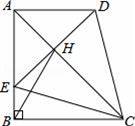
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的是 .(填序号)
①AC⊥DE;②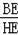
 =
=
 ;③CD=2DH;④
;③CD=2DH;④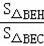
 =
=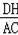
 .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
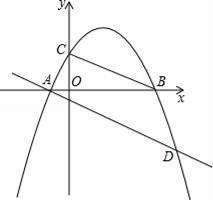
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点.
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com