
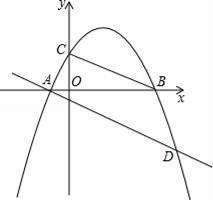
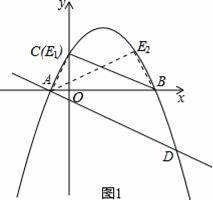
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点.
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.

【考点】二次函数综合题;一次函数的应用;勾股定理的应用;等腰直角三角形;矩形的性质;相似三角形的应用.
【专题】代数几何综合题;压轴题.
【分析】(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx+2,再根据过A,B两点,即可得出结果;
(2)由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.由相似关系求出点E的坐标;
(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,由BC∥AD设BC的解析式为y=kx+b,设AD的解析式为y=kx+n,由待定系数法求出一次函数的解析式,就可以求出点D坐标,由勾股定理就可以求出BD的值,由勾股定理的逆定理就可以得出∠ACB=90°,由平行线的性质就可以得出∠CAD=90°,就可以得出四边形ACBF是矩形,就可以得出BF的值,由勾股定理求出DF的值,而得出DF=BF而得出结论.
【解答】解:(1)∵该抛物线过点C(0,2),
∴可设该抛物线的解析式为y=ax2+bx+2.
将A(﹣1,0),B(4,0)代入,
得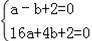
 ,
,
解得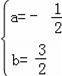
 ,
,
∴抛物线的解析式为:y=﹣
 x2+
x2+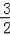
 x+2.
x+2.
(2)存在.
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.

在Rt△BOC中,OC=2,OB=4,
∴BC=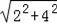
 =
=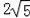
 .
.
在Rt△BOC中,设BC边上的高为h,则
 ×
×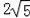
 h=
h=
 ×2×4,
×2×4,
∴h=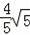
 .
.
∵△BEA∽△COB,设E点坐标为(x,y),
∴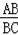
 =
=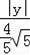
 ,
,
∴y=±2
将y=2代入抛物线y=﹣
 x2+
x2+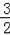
 x+2,
x+2,
得x1=0,x2=3.
当y=﹣2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,


∴∠BED=∠BFD=∠AFB=90°.
设BC的解析式为y=kx+b,由图象,得
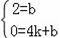
 ,
,
∴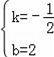
 ,
,
yBC=﹣
 x+2.
x+2.
由BC∥AD,设AD的解析式为y=﹣
 x+n,由图象,得
x+n,由图象,得
0=﹣
 ×(﹣1)+n
×(﹣1)+n
∴n=﹣
 ,
,
yAD=﹣
 x﹣
x﹣
 .
.
∴﹣
 x2+
x2+
 x+2=﹣
x+2=﹣
 x﹣
x﹣
 ,
,
解得:x1=﹣1,x2=5
∴D(﹣1,0)与A重合,舍去;
∴D(5,﹣3).
∵DE⊥x轴,
∴DE=3,OE=5.
由勾股定理,得BD=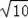
 .
.
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2.
∴AB=5
在Rt△AOC中,Rt△BOC中,由勾股定理,得
AC=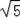
 ,BC=2
,BC=2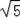
 ,
,
∴AC2=5,BC2=20,AB2=25,
∴AC2+BC2=AB2
∴△ACB是直角三角形,
∴∠ACB=90°.
∵BC∥AD,
∴∠CAF+∠ACB=180°,
∴∠CAF=90°.
∴∠CAF=∠ACB=∠AFB=90°,
∴四边形ACBF是矩形,
∴AC=BF=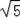
 ,
,
在Rt△BFD中,由勾股定理,
得DF=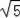
 ,
,
∴DF=BF,
∴∠ADB=45°.
【点评】本题考查了运用待定系数法求二次函数解析式和一次函数的解析式的运用,相似三角形的性质的运用,勾股定理的运用,矩形的判定及性质的运用,等腰直角三角形的性质的运用,解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:
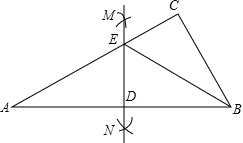
如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于 AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是 (填编号)


查看答案和解析>>
科目:初中数学 来源: 题型:
每年9月举行“全国中学生数学联赛”,成绩优异的选手可参加“全国中学生数学冬令营”,冬令营再选拔出50名优秀选手进入“国家集训队”.第31界冬令营已于2015年12月在江西省鹰谭一中成功举行.现将脱颖而出的50名选手分成两组进行竞赛,每组25人,成绩整理并绘制成如下的统计图: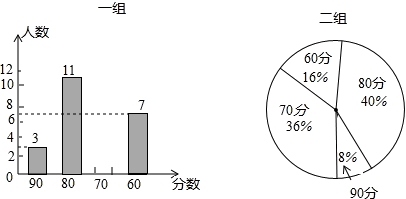
请你根据以上提供的信息解答下列问题:
(1)请你将表格补充完整:
| 平均数 | 中位数 | 众数 | 方差 | |
| 一组 | 74 | __________ | __________ | 104 |
| 二组 | __________ | __________ | __________ | 72 |
(2)从本次统计数据来看,__________组比较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com